Chọn C.
Hình hộp chữ nhật ABCD. A’B’C’D’ có 3 mặt đối xứng, đó là các mặt phẳng trung trực AB, AD, AA’.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có các kích thước là
a
,
b
,
c
(
a
b
c
)
.
Hình hộp chữ nhật này có mấy mặt đối xứng A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có các kích thước là a , b , c ( a < b < c ) . Hình hộp chữ nhật này có mấy mặt đối xứng
A. 1
B. 2
C. 3
D. 4
Hình hộp chữ nhật có ba kích thước là 3, 3, 4. Số mặt phẳng đối xứng của hình chữ nhật đó là
Đọc tiếp
Hình hộp chữ nhật có ba kích thước là 3, 3, 4. Số mặt phẳng đối xứng của hình chữ nhật đó là
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:A.
π
(
a
2
+
b
2
+
c
2
) B. 2
π
(
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Một hình hộp chữ nhật có ba kích thước là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tâm của mặt cầu (S) là
A. Một đỉnh bất kì của hình hộp chữ nhật.
B. Tâm của một mặt bên của hình hộp chữ nhật.
C. Trung điểm của một cạnh của hình hộp chữ nhật.
D. Tâm của hình hộp chữ nhật.
I. Trắc nghiệm ( 6 điểm)Một hình hộp chữ nhật có ba kích thước là a, b,c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, b, c. A.
π
a
2
+
b
2
+
c
2
B.
2
π
a...
Đọc tiếp
I. Trắc nghiệm ( 6 điểm)
Một hình hộp chữ nhật có ba kích thước là a, b,c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, b, c.
A. π a 2 + b 2 + c 2
B. 2 π a 2 + b 2 + c 2
C. 4 π a 2 + b 2 + c 2
D. π 2 a 2 + b 2 + c 2
Một hình hộp chữ nhật có ba kích thước là
a
,
b
,
c
. Thể tích
V
của khối hộp chữ nhật đó bằng A.
a
+
c
b
B.
a
b
c
C.
a
+
b
c
D.
1
3
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước là a , b , c . Thể tích V của khối hộp chữ nhật đó bằng
A. a + c b
B. a b c
C. a + b c
D. 1 3 a b c
Cho hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là a, b, c. Khi đó bán kính r của mặt cầu bằng
Đọc tiếp
Cho hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là a, b, c. Khi đó bán kính r của mặt cầu bằng
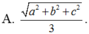
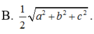
Một hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là a, b, c. Khi đó bán kính của mặt cầu bằng
Đọc tiếp
Một hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là a, b, c. Khi đó bán kính của mặt cầu bằng
Cho hình hộp chữ nhật
A
B
C
D
.
A
1
B
1
C
1
D
1
có ba kích thước
A
B...
Đọc tiếp
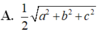
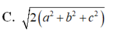
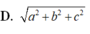
Cho hình hộp chữ nhật A B C D . A 1 B 1 C 1 D 1 có ba kích thước A B = a , A D = b , A A 1 = c . Trong các kết quả sau, kết quả nào là sai?
A. Khoảng cách giữa hai đường thẳng AB và C 1 C bằng b
B. Khoảng cách từ A đến mặt phẳng ( B 1 B D ) bằng a b a 2 + b 2 .
C. Khoảng cách từ A đến mặt phẳng ( B 1 B D ) bằng a b c a 2 + b 2 + c 2
D. B D 1 = a 2 + b 2 + c 2 .