Đáp án A
Tam giác ABB’ vuông tại B ⇒ B B ' = A B ' 2 − A B 2 = 2 a ⇒ A A ' = 2 a .
Thể tích khối hộp A B C D . A ' B ' C ' D ' là V = 2 2 a 3
Đáp án A
Tam giác ABB’ vuông tại B ⇒ B B ' = A B ' 2 − A B 2 = 2 a ⇒ A A ' = 2 a .
Thể tích khối hộp A B C D . A ' B ' C ' D ' là V = 2 2 a 3
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD).
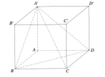
A. 5 91 49
B. 3 14 49
C. 9 14 98
D. 11 70 98
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a, AD=b, AA’=c. Tính thể tích V của khối chóp A.A’B’C’D’
A. V = 1 6 a b c
B. V = a b c
C. V = 1 3 a b c
D. V = 1 2 a b c
Cho hình hộp chữ nhật ABCD.A' B' C' D' có các kích thước là AB=2, AD=3, AA'=4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB' A' và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là
A. 5 π
B. 13 π 3
C. 8 π
D. 25 π 6
Tính thể tích V của khối lập phương ABCD.A' B' C' D' , biết AC'=a 3
A. V= 3 3 a 3
B. V= 27 a 3
C. V= a 3
D. V= 3 a 3
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
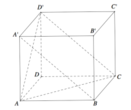
A. 2 10 7
B. 3 7
C. 3 35 35
D. 910 35
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'= 3 . Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
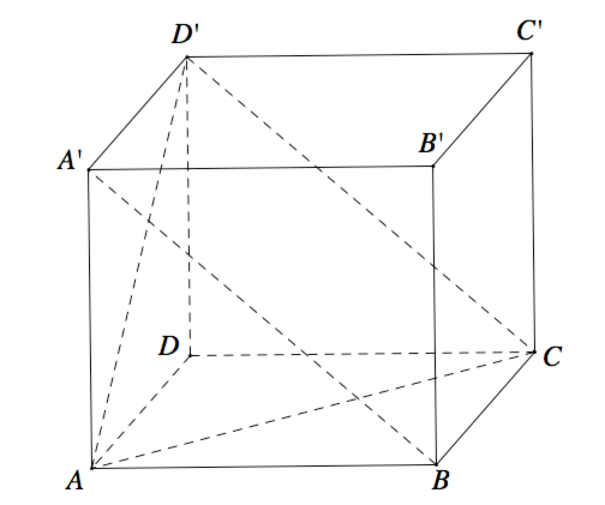
A. 57 19
B. 4 19 19
C. 6 4
D. 10 4
Cho hình hộp ABCD.A’B’C’D’ có A(1;0;0), B(2;-1;1), D(0;1;1) và A’(1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thànhbởi sáu điểm M, N, P, Q, E, F.
A. V = 1 3
B. V = 1 2
C. V = 2 3
D. V = 1
Một hình hộp chữ nhật có ba kích thước là a, b, c. Thể tích V của khối hộp chữ nhật đó bằng
A.(a+b)c
B. 1 3 a b c
C. abc
D.(a+c)b