Phương trình tiếp tuyến của đồ thị hàm số y = ln x 2 - x + 1 tại điểm có hoành độ x =1.
A. y = x - 1 .
B. y = x + 1 .
C. y = x + 1 - ln 3 .
D. y = x - 1 + ln 3 .
Phương trình tiếp tuyến của đồ thị hàm số y = ln(x2 – x +1) tại điểm có hoành độ x=1
A. y = x – 1
B. y = x + 1
C. y = x – 1 + ln3
D. y = x + 1 – ln3
Đáp án A.
Phương pháp: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x0 là: ![]()
Cách giải: Ta có: 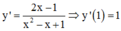
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1 là: ![]()
Viết phương trình tiếp tuyến của đồ thị hàm số sau:
a) \(y = {x^3} - 3{x^2} + 4\) tại điểm có hoành độ \({x_0} = 2\)
b) \(y = \ln x\) tại điểm có hoành độ \({x_0} = e\)
c) \(y = {e^x}\) tại điểm có hoành độ \({x_0} = 0\)
a) \(y' = \left( {{x^3} - 3{x^2} + 4} \right)' = 3{x^2} - 6x\), \(y'\left( 2 \right) = {3.2^2} - 6.2 = 0\)
Thay \({x_0} = 2\) vào phương trình \(y = {x^3} - 3{x^2} + 4\) ta được: \(y = {2^3} - {3.2^2} + 4 = 0\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 0.(x - 2) + 0 = 0\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là y = 0
b) \(y' = \left( {\ln x} \right)' = \frac{1}{x}\), \(y'(e) = \frac{1}{e}\)
Thay \({x_0} = e\) vào phương trình \(y = \ln x\) ta được: \(y = \ln e = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = \frac{1}{e}.\left( {x - e} \right) + 1 = \frac{1}{e}x - 1 + 1 = \frac{1}{e}x\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = \frac{1}{e}x\)
c) \(y' = \left( {{e^x}} \right)' = {e^x},\,\,y'(0) = {e^0} = 1\)
Thay \({x_0} = 0\) vào phương trình \(y = {e^x}\) ta được: \(y = {e^0} = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 1.\left( {x - 0} \right) + 1 = x + 1\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = x + 1\)
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
Ta có : \(y=\dfrac{x-1}{x+1}\Rightarrow y'=\dfrac{\left(x+1\right)-\left(x-1\right)}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}\)
Giả sử d' là tiếp tuyến của đths đã cho . Do d' // d : y = \(\dfrac{x-2}{2}\)
\(\Rightarrow d'\) có HSG = 1/2 \(\Rightarrow\dfrac{2}{\left(x+1\right)^2}=\dfrac{1}{2}\Leftrightarrow4=\left(x+1\right)^2\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với x = 1 . PTTT d' : \(y=\dfrac{1}{2}\left(x-1\right)+0=\dfrac{1}{2}x-\dfrac{1}{2}\)
Với x = -3 . PTTT d' : \(y=\dfrac{1}{2}\left(x+3\right)+2=\dfrac{1}{2}x+\dfrac{7}{2}\)
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
y'=(x-1)'(x+1)-(x-1)(x+1)'/(x+1)^2=(x+1-x+1)/(x+1)^2=2/(x+1)^2
(d1)//(d)
=>(d1): y=1/2x+b
=>y'=1/2
=>(x+1)^2=4
=>x=1 hoặc x=-3
Khi x=1 thì f(1)=0
y-f(1)=f'(1)(x-1)
=>y-0=1/2(x-1)=1/2x-1/2
Khi x=-3 thì f(-3)=(-4)/(-2)=2
y-f(-3)=f'(-3)(x+3)
=>y-2=1/2(x+3)
=>y=1/2x+3/2+2=1/2x+7/2
Cho hàm số y = x − 1 x + 2 . Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với trục Ox là
A. y = x + 3 y − 1 = 0
B. y = x + 3 y + 1 = 0
C. y = x − 3 y + 1 = 0
D. y = x − 3 y − 1 = 0
Đáp án D.
Có x − 1 x + 2 = 0 ⇔ x = 1. Có y ' = 3 x + 2 2
Giao với đồ thị hàm số với trục Ox là 1 ; 0 .
Phương trình tiếp tuyến tại 1 ; 0 . có phương trình là:
y = y ' 1 x − 1 + y 1 = 1 3 x − 1 ⇔ x − 3 y − 1 = 0
Cho hàm số y = x - 1 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d : y = x - 2 2
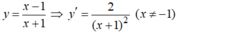
d: 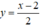 có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
- Gọi ( x 0 , y 0 ) là toạ độ của tiếp điểm.
- Ta có:
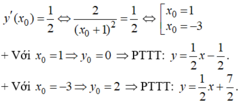
Đề bài
Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)
a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)
Cho hàm số y = x - 1 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = – 2.
Hệ số góc của tiếp tuyến với đồ thị hàm số y = ln(x+1) tại điểm có hoành độ x = 2 là
A. 1 3 ln 2
B. 1
C. ln2
D. 1 3
Cho hàm số y = x 3 − x + 2 có đồ thị (C). Phương trình tiếp tuyến của đồ thị (C) tại điểm M(1;2) là
A. y = 2x -1
B. y = 2x + 1
C. y = 2x - 4
D. y = 2x
Đáp án D
y ' = 3 x 2 − 1 ⇒ y ' 1 = 3 .1 2 − 1 = 2
Phương trình tiếp tuyến của (C) tại điểm M(1;2) là: y = y ' 1 . x − 1 + 2 hay y = 2x.