Phát biểu định lí về dấu của tam thức bậc hai.

Những câu hỏi liên quan
Phát biểu định lí về dấu của tam thức bậc hai
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x = , với mọi x ≠
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
Đúng 0
Bình luận (0)
Phát biểu định lý về dấu của một tam thức bậc hai \(f\left(x\right)=ax^2+bx+c\)
Cách nhận biết đa thức
\(f\left(x\right)=ax^2+bx+c\)
Có nghiệm hay vô nghiệm
Lập \(\Delta\) ( đọc là delta )
\(\Delta=b^2-4ac\)
Nếu \(\Delta< 0\) : đa thức vô nghiệm
Nếu \(\Delta\ge0\) : đa thức có nghiệm
Nếu \(\Delta>0\) : đa thức có hai nghiệm
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)
Đúng 0
Bình luận (0)
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh (Vẽ hình)Câu 2: Phát biểu định lí hai góc đối đỉnhCâu 3: phát biểu định nghĩa hai đường thẳng vuông gócCâu 4: Phát biểu định nghĩa đường trung trực của đoạn thẳngCâu 5: Phát biểu dấu hiệu (định lí) nhận bik hai đường thẳng song songCâu 6: Phát biểu tiên đề ơ clít về đường thẳng song songCâu 7: Phát biểu tính chất (định lí) của hai đường thẳng song songCâu 8: Phát biểu định lí về hai đường thẳng phân biệt với một đường thẳng số 3Câu 9: Phát biểu định l...
Đọc tiếp
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh (Vẽ hình)
Câu 2: Phát biểu định lí hai góc đối đỉnh
Câu 3: phát biểu định nghĩa hai đường thẳng vuông góc
Câu 4: Phát biểu định nghĩa đường trung trực của đoạn thẳng
Câu 5: Phát biểu dấu hiệu (định lí) nhận bik hai đường thẳng song song
Câu 6: Phát biểu tiên đề ơ clít về đường thẳng song song
Câu 7: Phát biểu tính chất (định lí) của hai đường thẳng song song
Câu 8: Phát biểu định lí về hai đường thẳng phân biệt với một đường thẳng số 3
Câu 9: Phát biểu định lí về hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba
Câu 10: Phát biểu định lí về một đường thẳng vuông góc với một đường thẳng song song
Câu 11: Phát biểu định lí về tổng ba góc của một tam giác
Câu 12: phát biểu tính chất góc ngoài của tam giác, phát biểu ba trường hợp bằng nhau của tam giác
Câu 13: phát biểu các trường hợp bằng nhau của tam giác vuông
(Mọi người ơi mọi người giúp em mấy câu hỏi này với😅Thank you m.n)
vote cho mk xong rồi mk trả lời cho, tin mk đi, mk ko phải n xấu đâu
Cho a, b, c là độ dài ba cạnh của tam giác. Sử dụng định lí về dấu tam thức bậc hai, chứng mình rằng:
b2x2 - (b2 + c2 - a2)x + c2 > 0 ∀x
Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).
Đúng 0
Bình luận (0)
( Tiếp theo )5. Phát biểu dấu hiệu ( định lí ) nhận biết hai đường thẳng song song.6. Phát biểu tiên đề Ơ-clit về đường thẳng song song.7. Phát biểu định lí về hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.8. Phát biểu tính chất ( định lí ) của hai đường thẳng song song.
Đọc tiếp
( Tiếp theo )
5. Phát biểu dấu hiệu ( định lí ) nhận biết hai đường thẳng song song.
6. Phát biểu tiên đề Ơ-clit về đường thẳng song song.
7. Phát biểu định lí về hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.
8. Phát biểu tính chất ( định lí ) của hai đường thẳng song song.
5. Dấu hiệu ( định lí ) nhận biết 2 đường thẳng song song:
+ Nếu đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có 1 cặp góc so le trong bằng nhau ( hoặc góc đồng vị bằng nhau ) thì a và b song song với nhau
6. Tiên đề Ơ - clit về đường thẳng song song:
Qua 1 điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
7, Định lí về hài đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3
Nếu 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau
8. Tính chất ( định lí ) của 2 đường thẳng song song:
Nếu 1 đường thẳng cắt 2 đường thẳng song song thì
1. Hai góc đồng vị bằng nhau
2. Hai góc so le trong bằng nhau
3. Hai góc trong cùng phía bù nhau
Đúng 0
Bình luận (0)
5. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
\(\widehat{A_1}=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
\(\widehat{A}_3=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
\(\widehat{A}_2+\widehat{B}_1=180^0\Rightarrow a//b\)
Đúng 0
Bình luận (0)
6.Qua một điểm nằm ngoài đường thẳng,chỉ có một đường thẳng song song với đường thẳng đó
7. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau \(\hept{\begin{cases}a\perp b\\b\perp c\end{cases}\Rightarrow}a//b\)
8.Nếu một đường thẳng cắt hai đường thẳng // thì :
a, 2 góc so le trong bằng nhau
b, 2 góc đồng vị bằng nhau
c, 2 góc trong cùng phía bù nhau
Đúng 0
Bình luận (0)
Phát biểu định lí về ba trường hợp đồng dạng của hai tam giác.
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Đúng 0
Bình luận (0)
a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} + 2x + 1b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai fleft( x right) - {x^2} + 4x - 4c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số a trong trường hợp Delta 0.
Đọc tiếp
a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\)
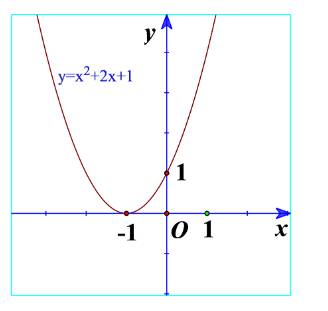
b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\)
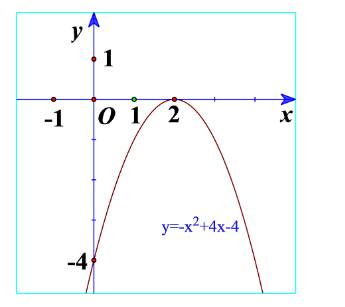
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta = 0\).
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)
Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)
Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)
Đúng 0
Bình luận (0)
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} - 2x + 2b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai fleft( x right) - {x^2} + 4x - 5c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số a trong trường hợp Delta 0.
Đọc tiếp
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - 2x + 2\)
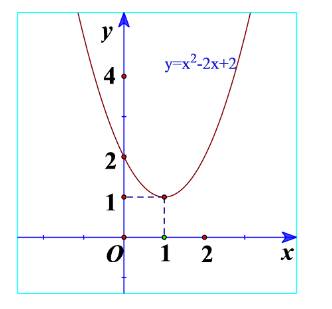
b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 5\)
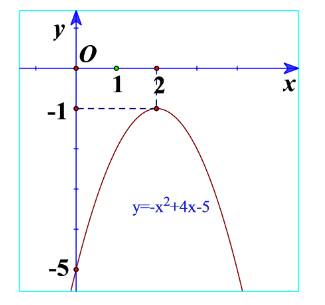
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta < 0\).
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.
Đúng 0
Bình luận (0)
Phát biểu các định lí về ba trường hợp đồng dạng của hai tam giác ?
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Đúng 0
Bình luận (0)
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Đúng 0
Bình luận (0)



















