Question

Cho a, b, c là độ dài ba cạnh của tam giác. Sử dụng định lí về dấu tam thức bậc hai, chứng mình rằng:

      b2x2 - (b2 + c2 - a2)x + c2 > 0 ∀x

Answer 1

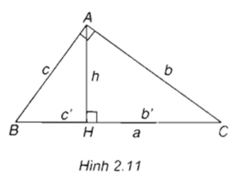
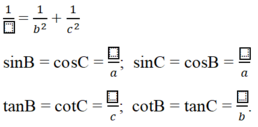Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:

Δ = (b2 + c2 - a2)2 - 4b2c2

    = (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)

    = [(b - c)2 - a2][(b + c)2 - a2]

    = (b – c – a)(b – c + a)(b + c + a)(b + c – a).

Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:

    b < c + a ⇒ b – c – a < 0

    c < a + b ⇒ b – c + a > 0

    a < b + c ⇒ b + c – a > 0

    a, b, c > 0 ⇒ a + b + c > 0

⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).