Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .
Tính giá trị nhỏ nhất của biểu thức T = x + y .
![]()
![]()
![]()
![]()
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .Tính giá trị nhỏ nhất của biểu thức T = x + y
![]()
![]()
![]()
![]()
Đáp án B.
Từ giả thiết, suy ra
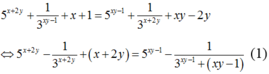
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
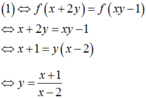
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
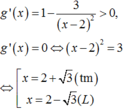
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
cho x,y,z là các số thực dương thỏa mãn điều kiện x+y+z=xyz.Tìm GTNN của biểu thức S=x/y^2 + y/z^2 + z/x^2
M=x+yxy.1z≥2√xyxy.1z=2z√xy≥2z(x+y2)=4z(x+y)M=x+yxy.1z≥2xyxy.1z=2zxy≥2z(x+y2)=4z(x+y)
=4z(1−z)=414−(z−12)2≥16=4z(1−z)=414−(z−12)2≥16
Min M= 16 khi z=1/2 và x=y =1/4
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 − x − 2 y + y x − 2 . Tính giá trị nhỏ nhất của biểu thức T=x+y
A. T min = 2 + 3 2
B. T min = 3 + 2 3
C. T min = 3 2
D. T min = 5 + 3 2
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y x - 2 . Tính giá trị nhỏ nhất của biểu thức T = x + y
A. T m i n = 2 + 3 2
B. T m i n = 3 + 2 3
C. T m i n = 1 + 5
D. T m i n = 5 + 3 2
Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .
Cho x,y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y x - 2
Tính giá trị nhỏ nhất của biểu thức T =x + y.
A. T m i n = 2 + 3 2
B. T m i n = 3 + 2 3
C. T m i n = 1 + 5
D. T m i n = 5 + 3 2
Từ giả thiết ta suy ra
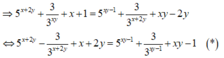
Xét hàm số f ( t ) = 5 t - 1 3 t + t với t ∈ ℝ , f ' ( t ) = 5 t . ln 5 + 3 - t . ln 3 + 1 > 0 ; ∀ t ∈ ℝ
Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra
f (x+ 2y) =f( xy-1) hay x+ 2y= xy-1
![]()
với x>0 suy ra y>1.
Khi đó
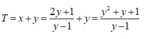
Xét hàm số
f ( y ) = y 2 + y + 1 y - 1 t r ê n 1 ; + ∞ f ' y = y 2 - 2 y - 2 y - 1 2 = 0 ⇔ y = ± 1 + 3 f 1 + 3 = 3 + 2 3 ; lim y → 1 f ( y ) = lim y → + ∞ f ( y ) = + ∞
Do đó, giá trị nhỏ nhất của hàm số là 3 + 2 3 .
Vậy kết quả là 3 + 2 3
Chọn B.
Cho x,y là các số thực dương thỏa mãn điều kiện x+y+xy=15. Tìm min của \(P=x^2+y^2\)
Vì x,y là số thực dương nên theo BĐT Cosi ta có:
\(x+y\ge2\sqrt{xy}\) Dấu "=" xảy ra <=> x=y hay x+x+x2=15 => x=y=3
GT: x+y+xy=15 => xy=15-(x+y)
Do đó: \(P=x^2+y^2=\left(x+y\right)^2-2xy=\left(x+y\right)^2-30+2\left(x+y\right)\ge\left(2\sqrt{xy}\right)^2-30+2\cdot2\sqrt{xy}\)
Dấu "=" xảy ra <=> x=y=3
Vậy \(min_P=4\cdot3^2-30+4\cdot3=18\Leftrightarrow x=y=3\)
Bài 1 :Cho 2 số dương x,y thỏa mãn điều kiện \(x+y\le1\). Chứng minh\(x^2-\frac{3}{4x}-\frac{x}{y}\le\frac{-9}{4}\)
Bài 2 : Cho 2 số thực x,y thay đổi thỏa mãn điều kiện x+y\(\ge1\)và x>0
Tìm giá trị nhỏ nhất của biểu thức \(M=y^2+\frac{8x^2+y}{4x}\)
bài 3: cho 3 số dương x,y,z thay đổi luôn thỏa mãn điều kiện x+y+z=1. Tìm giá trị lớn nhất của biểu thức:\(P=\dfrac{x}{x+1}+\dfrac{y}{y+1}+\dfrac{z}{z+1}\)
3: \(P=\dfrac{x}{\left(x+y\right)+\left(x+z\right)}+\dfrac{y}{\left(y+z\right)+\left(y+x\right)}+\dfrac{z}{\left(z+x\right)+\left(z+y\right)}\le\dfrac{1}{4}\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}\right)+\dfrac{1}{4}\left(\dfrac{y}{y+z}+\dfrac{y}{y+x}\right)+\dfrac{1}{4}\left(\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)=\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = x = \(\dfrac{1}{3}\).
Cho các số thực dương x,y thỏa mãn điều kiện căn(xy)×(x-y)=(x+y)
Tìm Min x+y
Giả sử x,y là các số thực dương thỏa mãn điều kiện \(\left(\sqrt{x}+1\right)\left(\sqrt{y}+1\right)>=4\)
Tìm Min
\(P=\dfrac{x^2}{y}+\dfrac{y^2}{x}\)
\(4\le\left(\sqrt{x}+1\right)\left(\sqrt{y}+1\right)\le\dfrac{1}{4}\left(\sqrt{x}+\sqrt{y}+2\right)^2\)
\(\Rightarrow\sqrt{x}+\sqrt{y}+2\ge4\)
\(\Rightarrow2\le\sqrt{x}+\sqrt{y}\le\sqrt{2\left(x+y\right)}\Rightarrow x+y\ge2\)
\(\Rightarrow P\ge\dfrac{\left(x+y\right)^2}{x+y}=x+y\ge2\)
Dấu "=" xảy ra khi \(x=y=1\)
Trước hết áp dụng BĐT: \(ab\le\dfrac{1}{4}\left(a+b\right)^2\)
Ta có: \(\left(\sqrt{x}+1\right)\left(\sqrt{y}+1\right)\le\dfrac{1}{4}\left(\sqrt{x}+1+\sqrt{y}+1\right)^2\)
Mà \(\left(\sqrt{x}+1\right)\left(\sqrt{y}+1\right)\ge4\Rightarrow\dfrac{1}{4}\left(\sqrt{x}+\sqrt{y}+2\right)^2\ge4\)
\(\Rightarrow\left(\sqrt{x}+\sqrt{y}+2\right)^2\ge4^2\)
\(\Rightarrow\sqrt{x}+\sqrt{y}+2\ge4\)
\(\Rightarrow\sqrt{x}+\sqrt{y}\ge2\)
Lại áp dụng tiếp: \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\Rightarrow a+b\le\sqrt{2\left(a^2+b^2\right)}\)
Ta được: \(\sqrt{x}+\sqrt{y}\le\sqrt{2\left(x+y\right)}\)
\(\Rightarrow\sqrt{2\left(x+y\right)}\ge\sqrt{x}+\sqrt{y}\ge2\)
Bình phương lên: \(2\left(x+y\right)\ge4\Rightarrow x+y\ge2\)
Phần cuối chắc là hoàn toàn cơ bản rồi