Cho khai triển 1 - 2 x n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n biết S = a 1 + 2 2 a 2 + . . . + n a n = 34992 Tính giá trị của biểu thức P = a 0 + 3 a 1 + 9 a 2 + . . . + 3 n a n
A. -78125
B. 9765625
C. -1953125
D. 390625
Những câu hỏi liên quan
2. Trong khai triển nhị thức ( a +2)^n +6 ( n€N). Có tất cả 17 số hạng . Vậy n bằng?
6. Trong khai triển (2a -1)^6 tổng 3 số hạng đầu là?
7. Trong khai triển ( x - √y )^16 tổng hai số hạng cuối là
2/ \(\left(a+b\right)^k\Rightarrow k+1\left(so-hang\right)\)
\(\Rightarrow n+6+1=17\Rightarrow n=10\)
6/ \(\left(2a-1\right)^6=\sum\limits^6_{k=0}C^k_6.2^{6-k}.\left(-1\right)^k.a^{6-k}\)
\(\Rightarrow tong-3-so-hang-dau=C^0_6.2^6+C^1_6.2^5.\left(-1\right)+C^2_6.2^4.\left(-1\right)^2=...\)
7/ \(\left(x-\sqrt{y}\right)^{16}=\left(x-y^{\dfrac{1}{2}}\right)^{16}\)
\(\Rightarrow tong-2-so-hang-cuoi=C^{16}_{16}+C^{15}_{16}=...\)
Đúng 0
Bình luận (0)
6 tháng 5 2023 lúc 16:04
Cho \(n\in N^{sao}\) thỏa \(C_n^1+C_n^2=15.\) Tìm số hạng không chứa \(x\) trong khai triển \(\left(x+\dfrac{2}{x^4}\right)^n\)
\(C^1_n+C^2_n=15\) (Điều kiện: \(n\ge2\))
\(\Leftrightarrow n+\dfrac{n!}{2!\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)\left(n-2\right)!}{2\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)}{2}=15\)
\(\Leftrightarrow2n+n\left(n-1\right)=30\)
\(\Leftrightarrow2n+n^2-n=30\)
\(\Leftrightarrow n^2+n-30=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=5\\n=-6\left(\text{loại}\right)\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{2}{x^4}\right)^5=C^k_5x^{5-k}\left(\dfrac{2}{x^4}\right)^k=C^k_5x^{5-k-4k}.2^k=C^k_5x^{5-5k}.2^k\)
\(ycbt\Leftrightarrow5-5k=0\Leftrightarrow k=1\)
\(\Rightarrow C^1_5.2^1=10\)
Vậy số hạng không chứa \(x\) trong khai triển là \(10\).
Đúng 0
Bình luận (0)
Cho khai triển
(
1
+
x
)
n
với n là số nguyên dương. Tìm hệ số của số hạng chứa
x
3
trong khai triển biết
C
2
n
+
1
1
+
C
2...
Đọc tiếp
Cho khai triển ( 1 + x ) n với n là số nguyên dương. Tìm hệ số của số hạng chứa x 3 trong khai triển biết C 2 n + 1 1 + C 2 n + 1 2 + C 2 n + 1 3 + . . . . . + C 2 n + 1 n = 2 20 - 1 .
A. 480
B. 720
C. 240
D. 120
Chọn D
Ta có: 
Ta có: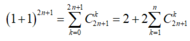 
Hệ số của số hạng chứa x 3 là: C 10 3 = 120.
Đúng 0
Bình luận (0)
Cho n là số nguyên dương thỏa mãn
A
n
2
-
3
C
n
n
-
1
11
n
. Xét khai triển
P
x
x
-
2
n...
Đọc tiếp
Cho n là số nguyên dương thỏa mãn A n 2 - 3 C n n - 1 = 11 n . Xét khai triển P x = x - 2 n . Hệ số chứa x 10 trong khai triển là:
A. 384384
B. -3075072
C. -96096
D. 3075072
Cho n là số nguyên dương thỏa mãn
A
n
2
-
3
C
n
n
-
1
11
n
. Xét khai triển
P
x...
Đọc tiếp
Cho n là số nguyên dương thỏa mãn A n 2 - 3 C n n - 1 = 11 n . Xét khai triển P x = x - 2 n . Hệ số chứa x 10 trong khai triển là:
A. 384384
B. - 3075072
C. - 96096
D. 3075072
Đáp án C
Phương pháp:
+) Công thức khai triển nhị thức Newton: 
+) 
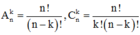
Cách giải:
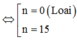
Với n =15: 
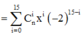
Hệ số chứa
x
10
ứng với i = 10 và bằng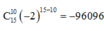 
Đúng 0
Bình luận (0)
Câu 2. (2 điểm) Cho biểu thức $Q=(x y-1)^5$.
a) Viết khai triển biểu thức $Q$ bằng nhị thức Newton.
b) Tìm số hạng có chứa $x^2 y^2$ trong khai triển trên.
1) tìm hệ số của x^5 trong khai triển x(2x−1)6+(3x−1)8
2) tìm hệ số của x3 trong khai triển x(1+2x)n với n t/mAnx=12
Cho khai triển (2x-1)^6.(3x^2+1)^5 . Tìm số hạng chứa x^4 trong khai triển .
\(\left(2x-1\right)^6\left(3x^2+1\right)^5=\sum\limits^6_{k=0}C_6^k\left(2x\right)^k\left(-1\right)^{6-k}\sum\limits^5_{i=0}C_5^i\left(3x^2\right)^i\)
\(=\sum\limits^6_{k=0}\sum\limits^5_{i=0}C_6^k.C_5^i.\left(-1\right)^{6-k}.2^k.3^i.x^{k+2i}\)
Số hạng chứa \(x^4\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le k\le6\\0\le i\le5\\k+2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(0;4\right);\left(1;2\right);\left(2;0\right)\)
Hệ số:
\(C_6^4.C_5^0\left(-1\right)^4.2^4.3^0+C_6^2C_5^1\left(-1\right)^2.2^2.3^1+C_6^0.C_5^2.\left(-1\right)^0.2^0.3^2=...\)
Đúng 0
Bình luận (0)
Biết tổng các hệ số của ba số hạng đầu trong khai triển \(\left(x^3+\dfrac{1}{x^2}\right)^n\) bằng 11. Tìm hệ số của \(x^7\) trong khai triển đó.
\(C_n^0+C_n^1+C_n^2=11\)
\(\Rightarrow1+n+\dfrac{n\left(n-1\right)}{2}=11\)
\(\Leftrightarrow n^2+n-20=0\Rightarrow\left[{}\begin{matrix}n=4\\n=-5\left(loại\right)\end{matrix}\right.\)
\(\left(x^3+\dfrac{1}{x^2}\right)^4\) có SHTQ: \(C_4^k.x^{3k}.x^{-2\left(4-k\right)}=C_4^k.x^{5k-8}\)
\(5k-8=7\Rightarrow k=3\)
Hệ số: \(C_4^3=4\)
Đúng 0
Bình luận (0)
Cho khai triển nhị thức Niuton
x
2
+
2
n
x
n
với n
n
∈
ℕ
, x 0. Biết rằng số hạng thứ 2 của khai triển bằng 98 và n thỏa mãn
A
n...
Đọc tiếp
Cho khai triển nhị thức Niuton x 2 + 2 n x n với n n ∈ ℕ , x > 0. Biết rằng số
hạng thứ 2 của khai triển bằng 98 và n thỏa mãn A n 2 + 6 C n 3 = 36 n Trong các giá trị x sau, giá trị nào thỏa mãn?
A. 3
B. 4
C. 1
D. 2
