Đáp án C
Phương pháp:
+) Công thức khai triển nhị thức Newton: 
+) 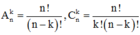
Cách giải:

![]()
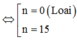
Với n =15: ![]()
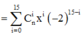
Hệ số chứa
x
10
ứng với i = 10 và bằng 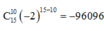
Đáp án C
Phương pháp:
+) Công thức khai triển nhị thức Newton: 
+) 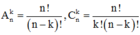
Cách giải:

![]()
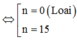
Với n =15: ![]()
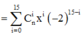
Hệ số chứa
x
10
ứng với i = 10 và bằng 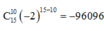
Xét n là số nguyên dương thỏa mãn điều kiện C n + 4 n + 1 - C n + 3 n = 7 n + 3 . Hệ số của số hạng chứa x 8 trong khai triển 1 x 3 + x 5 n với x > 0, bằng
A. 549
B. 954
C. 945
D. 495
Cho n là số nguyên dương thỏa mãn 3 C n 2 + 2 A n 2 = 3 n 2 + 15 . Tìm hệ số của số hạng chứa x 10 trong khai triển ( 2 x 3 - 3 x 2 ) n , x ≠ 0
A. 1088640
B. 1088460
C. 1086408
D. 1084608
Xét n là số nguyên dương thỏa mãn điều kiện
C n 1 + 2 C n 2 C n 1 + 3 C n 3 C n 2 + . . . + k C n k C n k - 1 + n C n n C n n - 1 = 55
Hệ số của số hạng chứa x trong khai triển của biểu thức 1 + x n bằng
A. 13
B. 12
C. 11
D. 10
Với số nguyên dương n thỏa mãn C n 2 − n = 27 , trong khai triển x + 2 x 2 n số hạng không chứa x là:
A. 84
B. 8
C. 5376
D. 672
Với các số nguyên dương n thỏa mãn C n 2 - n = 27 , trong khai triển x + 2 x 2 n số hạng không chứa x là:
A. 84
B. 8
C. 5376
D. 672
Xét n là số nguyên dương thỏa mãn điều kiện C n 1 + 3 C n 2 = 145 . Số hạng không chứa x trong khai triển của biểu thức x 4 - 3 x n , x ≠ 0 bằng
A. 295245
B. 59049
C. – 59049
D. – 295245
Cho n là số nguyên dương thỏa mãn 5 C n n - 1 - C n 3 = 0 . Tìm hệ số của số hạng chứa x 5 trong khai triển nhị thức Niu-tơn của x 2 2 - 1 x n , x ≢ 0
A. - 35 16 x 5
B. - 35 16
C. - 35 16 x 2
D. 35 16 x 5
Cho số n nguyên dương và thỏa mãn C n 0 + 2 C n 1 + 4 C n 2 + . . . . + 2 n C n n = 243 Tìm hệ số của x 2 trong khai triển ( 1 + x ) n
A. 4
B. 5
C. 15
D. 10
Cho n là số nguyên dương thỏa mãn 3 n C n 0 − 3 n − 1 C n 1 + 3 n − 2 C n 2 − ... + − 1 n C n n = 2048. Hệ số của x 10 trong khai triển x + 2 n là
A. 11264
B. 22
C. 220
D. 24