Đáp án D.
Phương pháp
Sử dụng công thức C n k = n ! k ! n − k ! tìm n.
Sử dụng khai triển nhị thức Newton
a + b n = ∑ k = 0 n C n k . a n − k . b k
Cách giải
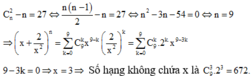
Đáp án D.
Phương pháp
Sử dụng công thức C n k = n ! k ! n − k ! tìm n.
Sử dụng khai triển nhị thức Newton
a + b n = ∑ k = 0 n C n k . a n − k . b k
Cách giải
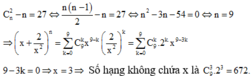
Với các số nguyên dương n thỏa mãn C n 2 - n = 27 , trong khai triển x + 2 x 2 n số hạng không chứa x là:
A. 84
B. 8
C. 5376
D. 672
Số hạng không chứa x trong khai triển 2 x - 3 x 3 2 n với x ≠ 0 , biết n là số nguyên dương thỏa mãn C n 3 + 2 n = A n + 1 2 là
A. - C 16 12 . 2 4 . 3 12
B. C 16 0 . 2 16
C. C 16 12 . 2 4 . 3 12
D. C 16 16 . 2 0
Tìm số hạng không chứa x trong khai triển 2 x - 3 x 3 2 n với x ≠ 0 , biết n là số nguyên dương thỏa mãn C n 3 + 2 n = A n + 1 2
A. - C 16 12 . 2 4 . 3 12
B. C 16 0 . 2 16
C. C 16 12 . 2 4 . 3 12
D. C 16 16 . 2 0
Tìm số hạng không chứa x trong khai triển 2 x - 3 x 3 2 n với x ≠ 0 , biết n là số nguyên dương thỏa mãn C n 3 + 2 n = A n + 1 2 .
A. - C 16 12 . 2 4 . 3 12 .
B. C 16 0 . 2 16 .
C. C 16 12 . 2 4 . 3 12 .
D. C 16 16 . 2 0
Cho n là số nguyên dương thỏa mãn C n 2 - C n 1 = 44 . Số hạng không chứa x trong khai triển của biểu thức x x + 1 x 4 n , với x > 0 bằng
A. 165
B. 485
C. 238
D. 525
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng:
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng:
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 3 + 2 x 2 n bằng
A. 322560
B. 3360
C. 80640
D. 13440
Với n là số nguyên dương thỏa mãn C n 1 + C n 2 = 55 , số hạng không chứa x trong khai triển của biểu thức x 2 + 2 x 2 n bằng.
A. 322560
B. 3360
C. 80640
D. 13440