Giải các phương trình trùng phương 1 3 x 4 - 1 2 x 2 + 1 6 = 0

Những câu hỏi liên quan
Giải các phương trình trùng phương sau: x 4 + 2 x 2 – x + 1 = 15 x 2 – x – 35
Ta có: x 4 + 2 x 2 – x + 1 = 15 x 2 – x – 35
⇔ x 4 + 2 x 2 – x + 1 - 15 x 2 + x + 35 = 0
⇔ x 4 – 13 x 2 + 36 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: x 4 – 13 x 2 + 36 = 0 ⇔ m 2 – 13m + 36 = 0
∆ = - 13 2 – 4.1.36 = 169 – 144 = 25 > 0
∆ = 25 = 5
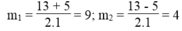
Ta có: x 2 = 9 ⇒ x = ± 3
x 2 = 4 ⇒ x = ± 2
Vậy phương trình đã cho có 4 nghiệm: x 1 = 3; x 2 = -3; x 3 = 2; x 4 = -2
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương:
a
)
x
4
−
5
x
2
+
4
0
b
)
2
x
4
−
3...
Đọc tiếp
Giải các phương trình trùng phương:
a ) x 4 − 5 x 2 + 4 = 0 b ) 2 x 4 − 3 x 2 − 2 = 0 c ) 3 x 4 + 10 x 2 + 3 = 0
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
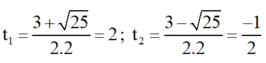
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
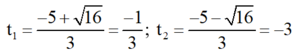
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương: x4 – 5x2 + 4 = 0
x4 – 5x2 + 4 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t2 – 5t + 4 = 0 (2)
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương:
3x4 + 10x2 + 3 = 0
3x4 + 10x2 + 3 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 3t2 + 10t + 3 = 0 (2)
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ’ = 52 – 3.3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
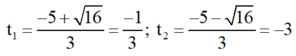
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương 3 x 4 – (2 - 3 ) x 2 -2 =0
Giải các phương trình trùng phương: 3x4 + 4x2 + 1 = 0
3x4 + 4x2 + 1 = 0
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
3t2 + 4t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t1 = -1; t2 = (-1)/3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
Đúng 0
Bình luận (0)
Giải phương trình trùng phương: 2 x 2 + 1 = 1 x 2 - 4
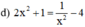
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2x4 + x2 = 1 – 4x2
⇔ 2x4 + x2 + 4x2 – 1 = 0
⇔ 2x4 + 5x2 – 1 = 0 (1)
Đặt t = x2, điều kiện t > 0.
Khi đó (1) trở thành : 2t2 + 5t – 1 = 0 (2)
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 52 – 4.2.(-1) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
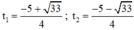
Đối chiếu với điều kiện thấy có nghiệm t1 thỏa mãn.
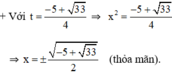
Vậy phương trình có tập nghiệm 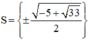
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương sau: 3 x 4 – 6 x 2 = 0
Ta có: 3 x 4 – 6 x 2 = 0 ⇔ 3 x 2 ( x 2 – 2) = 0
![]()
Vậy phương trình đã cho có 3 nghiệm: x 1 = 0; x 2 = -√2 ; x 3 = √2
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương sau: 2 x 4 + x 2 – 3 = x 4 + 6 x 2 + 3
Ta có: 2 x 4 + x 2 – 3 = x 4 + 6 x 2 + 3
⇔ 2 x 4 + x 2 – 3 – x 4 – 6 x 2 – 3 = 0
⇔ x 4 – 5 x 2 – 6 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: x 4 – 5 x 2 – 6 = 0 ⇔ m 2 – 5m – 6 = 0
∆ = - 5 2 – 4.1.(-6) = 25 + 24 = 49 > 0
∆ = 49 = 7
![]()
Ta có: x 2 = 6 ⇒ x = ± 6
Vậy phương trình đã cho có 2 nghiệm: x 1 = 6 , x 2 = - 6
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương 36 t 4 – 13 t 2 +1 = 0
Đặt m = t 2 .Điều kiện m ≥ 0
Ta có: 36 t 4 – 13 t 2 +1 = 0 ⇔ 36 m 2 -13m +1 =0
Ta có: ∆ = - 13 2 – 4.36.1=169 -144=25 > 0
∆ = 25 = 5
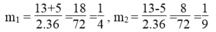
Ta có: t 2 =1/4 ⇒ t= ± 1/2
t 2 =1/9 ⇒ t= ± 1/3
Vậy phương trình đã cho có 4 nghiệm :
t 1 = 1/2 ; t 2 = -1/2 ; t 3 = 1/3 ; t 4 = -1/3
Đúng 0
Bình luận (0)


