cho tam giác abc có ab=cd . D là trung điểm
a)chứng minh ABD= ACD
b) AD song song BC

Những câu hỏi liên quan
Cho tam giác ABC có AB = AC. Gọi D là trung điểm cạnh BC qua A vẽ đường thẳng d song song với BC. Chứng minh rằng:
a) tam giác ABD = tam giác ACD
b) AD là tia phân giác của góc BAC
c) AD vuông góc với đường thẳng d
a) Xét \(\Delta\)ABD và \(\Delta\)ACD có:
AB = AC (gt)
AD: cạnh chung
BD = CD (D là trung điểm của BC)
\(\Rightarrow\Delta\)ABD = \(\Delta\)ACD (c.c.c)
b) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)
\(\Rightarrow\widehat{BAD}\) = \(\widehat{CAD}\) (2 góc tương ứng)
\(\Rightarrow\) AD là tia phân giác của \(\widehat{BAC}\)
c) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)
\(\Rightarrow\widehat{ADB}\) =\(\widehat{ADC}\) (2 góc tương ứng)
mà \(\widehat{ADB}\) + \(\widehat{ADC}\) = 18001800 (2 góc kề bù)
\(\Rightarrow\widehat{ADB}\) = \(\widehat{ADC}\) = 900900
\(\Rightarrow\) AD \(\perp\) BC
Lại có: d // BC (gt) \(\Rightarrow\) AD \(\perp\) d
ĐS:......................
#Châu's ngốc
Cho tam giác ABC có ABAC . Tia phân giác góc A cắt BC tại D . a, Chứng minh tam giác ABD bằng tam giác ACD .b , Trên nửa mặt phẳng bờ BC chứa điểm A vẽ tia Cx vuông góc BC . Trên nửa mặt phẳng bờ chứa AB chứa điểm C vẽ tia AY song song BC . Chứng minh góc yAc góc ABC .c , Chứng minh AD song song Cx d, Gọi I là trung điểm của AC , K là giao điểm của 2 tia Ay và Cx . Chứng minh I là trung điểm của DK .
Đọc tiếp
Cho tam giác ABC có AB=AC . Tia phân giác góc A cắt BC tại D .
a, Chứng minh tam giác ABD bằng tam giác ACD .
b , Trên nửa mặt phẳng bờ BC chứa điểm A vẽ tia Cx vuông góc BC . Trên nửa mặt phẳng bờ chứa AB chứa điểm C vẽ tia AY song song BC . Chứng minh góc yAc = góc ABC .
c , Chứng minh AD song song Cx
d, Gọi I là trung điểm của AC , K là giao điểm của 2 tia Ay và Cx . Chứng minh I là trung điểm của DK .
cho tam giác ABC có AB = AC. Tia phân giác A cắt BC ở D. a) Chứng minh tam giác ABD = tam giác ACD và BD = DC b) chứng minh AD vuông với BC c) trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng BC vẽ tia Bx song song với AC. Trên cạnh AC lấy điểm E, trên tia Bx. Lấy điểm N sao cho CE = BN. Chứng minh ba điểm N,D,E thẳng hàng
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
Suy ra: BD=CD
b: Ta có: ΔABC cân tại A
mà AD là tia phân giác
nên AD là đường cao
Đúng 0
Bình luận (0)
cho tam giác ABC có ABAC tia phân giác của góc A cắt BC tại Da, chứng minh tam giác abd tam giác acdb, trên nủa mặt phẳng bời bc chứa điểm a vẽ tia cx vuông góc bc trên nửa mặt phẳng bờ ab chứa điểm c vẽ tia ay song song ac. chứng minh góc yac bằng góc abcc, chứng minh ad song song cxd, gọi I là trung điểm của ac. K là giao điểm của hai tia AI và Cx. chứng minh I là trung điểm của DK
Đọc tiếp
cho tam giác ABC có AB=AC tia phân giác của góc A cắt BC tại D
a, chứng minh tam giác abd = tam giác acd
b, trên nủa mặt phẳng bời bc chứa điểm a vẽ tia cx vuông góc bc trên nửa mặt phẳng bờ ab chứa điểm c vẽ tia ay song song ac. chứng minh góc yac bằng góc abc
c, chứng minh ad song song cx
d, gọi I là trung điểm của ac. K là giao điểm của hai tia AI và Cx. chứng minh I là trung điểm của DK
Bạn tự vẽ hình nhé
a) Xét \(\Delta ABD\)và\(\Delta ACD\)có:
AB = AC ( gt)
\(\widehat{BAD}=\widehat{CAD}\)(gt)
AD chung
\(\Rightarrow\)\(\Delta ABD=\Delta ACD\left(c.g.c\right)\)
Đúng 0
Bình luận (0)
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EFAB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.2. Cho tứ giác ABCD có ADBC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEMgóc MFB.3. Cho tam giác ABC (ABAC). Trên cạnh AB lấy điểm D sao cho BDAC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC 2.BMN4. Cho tứ giác ABCD, gọi A, B, C, D lần lượt là trọng tâm của các tam giác BCD,...
Đọc tiếp
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EF=AB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.
2. Cho tứ giác ABCD có AD=BC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEM=góc MFB.
3. Cho tam giác ABC (AB>AC). Trên cạnh AB lấy điểm D sao cho BD=AC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC = 2.BMN
4. Cho tứ giác ABCD, gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng các đường thẳng AA', BB', CC', DD' đồng quy.
5. Cho tam giác ABC, G là trọng tâm. Đường thẳng d không cắt các cạnh của tam giác ABC. Gọi A', B', C', G' lần lượt là hình chiếu của A, B, C, G trên đường thẳng d. Chứng minh GG'=AA'+BB'+CC'/3
Cho tám giác ABC có M là trung điểm của BC. Trên tia đối AM lấy điểm D sao cho M là trung điểm của AD: a) Chứng Minh tam giác ABM= tam giác DCM. b) Chứng minh AB song song CD. c) Qua C kẻ đường thẳng song song với AD cắt AB kéo dài tại E. Chứng minh A là trung điểm của BE
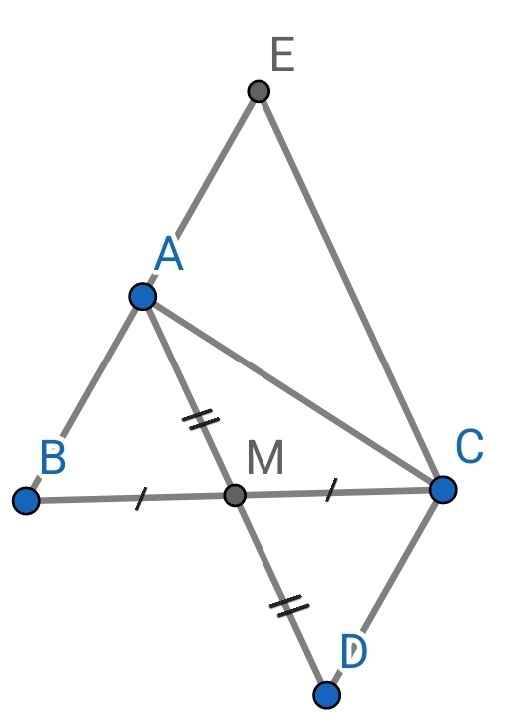 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE
Đúng 0
Bình luận (0)
Cho tam giác ABC có ABAC. Tia phân giác góc A cắt BC tại D .a)Chứng minh tam giác ABD tam giác ACDb)Trên nửa mf bờ bc chứa ddiemr A vẽ tia Cx vuông góc với BC. Trên nửa mf bờ chứa điểm C vẽ tia Ay song song với BC. Chứng minh widehat{yAC}widehat{ABC} c) Chứng minh AD song song với Cx d)Gọi I là trung điểm AC, K là giảo điểm của 2 tia Ay và Cx. Chứng minh I là trung điểm của DK
Đọc tiếp
Cho tam giác ABC có AB=AC. Tia phân giác góc A cắt BC tại D .
a)Chứng minh tam giác ABD= tam giác ACD
b)Trên nửa mf bờ bc chứa ddiemr A vẽ tia Cx vuông góc với BC. Trên nửa mf bờ chứa điểm C vẽ tia Ay song song với BC. Chứng minh \(\widehat{yAC}=\widehat{ABC}\)
c) Chứng minh AD song song với Cx
d)Gọi I là trung điểm AC, K là giảo điểm của 2 tia Ay và Cx. Chứng minh I là trung điểm của DK
Cho tam giác ABC cân tại A. Gọi D là trung điểm cạnh BC. Qua A vẽ đường thẳng d song song với BC. Chứng minh rằng:
a) t/giác ABD = t/giác ACD
b) AD là tia phân giác của góc BAC.
c) AD vuông góc với d.
xét∆ABD và∆ACD có:
BD=CD
AB=AC
Chung AD
=) ∆ABD=∆ACD( c-g-c )
b)do AB=AC =) ∆ABC cân tai A .
Lại có: BD=CD=)AD là trung tuyến∆ABC .
Suy ra AD là phân giác góc BAC
c) do trong∆ cân thì đường trung tuyến vừa là phân giác vừa là đường cao vừa là trung trực nên AD vuông góc với BC
=>AD vuông góc với BC
mà BC//d
=> AD vuông góc với d
Cho tam giác ABC có AB=AC. Gọi D là trung điểm cạnh BC, qua A vẽ đường thẳng d song song với BC. Chứng minh rằng:
a, tam giác ABD= tam giác ACD
b, AD là tia phân giác của góc BAC
c, AD vuông góc với đường thằng d
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
b: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là tia phân giác của góc BAC
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
=>AD⊥BC
mà d//BC
nên AD⊥d
Đúng 3
Bình luận (0)
a) Xét ΔΔABD và ΔΔACD có:
AB = AC (gt)
AD: cạnh chung
BD = CD (D là trung điểm của BC)
⇒Δ⇒ΔABD = ΔΔACD (c.c.c)
b)b) Ta có: ΔΔABD = ΔΔACD (theo ý a)
⇒\(\widehat{BAD}\)=\(\widehat{CAD}\) (2gocs tương ứng )
⇒ AD là tia phân giác của \(\widehat{BAC}\)
c) Ta có: ΔΔABD = ΔΔACD (theo ý a)
⇒ \(\widehat{ADB}\)=\(\widehat{ADC}\)(2 góc tương ứng )
mà \(\widehat{ADB}\) + \(\widehat{ADC}\)=18001800( 2 góc kề bù )
⇒\(\widehat{ADB}\)=\(\widehat{ADC}\)= 900900
⇒ AD ⊥ BC
Lại có: d // BC (gt) ⇒ AD ⊥ d
Đúng 0
Bình luận (0)



















