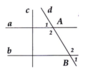
Trong hình bên cho c vuông góc với a, c vuông góc với b và A 2 ^ = 2 A 1 ^ . Tính số đo B 1 ^ và B 2 ^
1,Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy, SA=a√6,AB=a.
a/Chứng minh các mặt bên của hình chóp là các tam giác vuông
b/ Xác định và tính góc giữa đường thẳng SC và mặt đáy (ABC)
2,Cho hình chóp S. MNPQ là hình vuông cạnh a SM vuông góc với mặt phẳng (MNPQ),SM=a√2.
a/ Chứng minh QN vuông góc với mặt phẳng (SMP).
b/ Trong tam giác SMQ dựng đường cao MH, chứng minh MH vuông góc với SP.
c/ Xác định và tính khoảng cách giữa hai đường thẳng MN và SQ
GIÚP MÌNH VỚI Ạ
MÌNH CẢM ƠN 💙💙💙
1, Cho hình thang ABCD ( AB // CD ) có góc B - góc C = 24° , góc A = 1,5 góc D . Tính các góc của hình thang .
2. Cho hình thang vuông ABCD ( góc A = góc D = 90°) đường chéo BD vuông góc với cạnh bên BC và BD = BC :
a, Tính các góc của hình thang .
b, Biết AB = 3 cm , Tính độ dài các cạnh BC,CD .
Cho tứ giác A,B,C,D có số đo của các góc A,B,C,D lần lượt tỉ lệ với 1,2,3,4. CMR
a) Tứ giác ABCD là hình thang
b)2 tia phân giác góc A và góc D vuông góc với nhau, 2 tia phân giác góc B và C vuông góc với nhau
a) Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(Định lí tổng bốn góc trong một tứ giác)
mà \(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\dfrac{360^0}{10}=36^0\)
Do đó: \(\widehat{A}=36^0;\widehat{B}=72^0;\widehat{C}=108^0;\widehat{D}=144^0\)
Ta có: \(\widehat{B}+\widehat{C}=180^0\)
mà hai góc này là hai góc trong cùng phía
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)
hay ABCD là hình thang
Cho hình thang cân ABCD (AB//CD,AB>CD). CD=a và góc A + góc B=1/2 (góc C và D).Đường chéo AC vuông góc với cạnh bên AC. a) Tính các góc của hình thang
b)CM AC la phân giác của góc DAB
c)Tính diện tích hình thang
Cho hình thang vuông ABCD (góc A= góc D= 90 độ), đường chéo BD vuông góc với cạnh bên BC và bằng BC.
a) Tính các góc B và C của hình thang ABCD
b) CM: AB=AD
c)CM: CD=2AD
ét tam giác DBC có :
góc B = 90 độ ( BD vuông góc BC)
BD=BC
=> tam giác DBC là tam giác vuông cân => góc C =góc BDC= 45 độ
xét hình thang ABCD có :
góc ABC = 360 độ - ( 90 dộ+90 độ+45 độ) = 135 độ
b) ta có :
góc ABD = góc ABC - góc DBC = .135 độ - 90 độ = 45 độ
BD = cos ABD . AB = cos 45 độ . 3 = ......cm
mà BD=BC=> BC =.....cm
xét tam giác vuông cân DBC có
CD^2= BC^2 + BD^2 (định lí pi-ta-go)
<=>.................
<=>.................
=> CD =........cm
Cho hình vuông ABCD có cạnh bằng a. Một góc 45 độ quay xung quanh đỉnh A và nằm bên trong hình vuông cắt cạnh BC,CD lần lượt tại M và N.
1) C/m MN luôn tiếp xúc với một đường tròn cố định.
2) C/m a2- BM.DN=a(BM+DN)
Hình bên có:
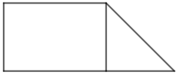
A. 1 góc bẹt, 1 góc tù, 5 góc vuông và 1 góc nhọn
B. 1 góc bẹt, 1 góc tù, 4 góc vuông và 2 góc nhọn
C. 1 góc bẹt, 3 góc vuông và 2 góc nhọn
D. 1 góc bẹt, 1 góc tù, 5 góc vuông và 2 góc nhọn
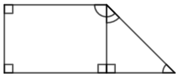
Ta thấy, hình vẽ trên có 1 góc bẹt, 1 góc tù 5 góc vuông và 2 góc nhọn
Chọn D
Cho góc ∠xOy = 120o. Kẻ Ot là tia phân giác của góc xOy. Kẻ tia Om nằm trong góc xOy và vuông góc với tia Ox. Kẻ tia On nằm trong góc xOy và vuông góc với tia Oy. Với hình vẽ được có bao nhiêu góc bằng 30o ?
(A) 3;
(B) 4;
(C) 2;
(D) 1.
Các góc có số đo bằng 30º là:
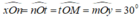
Chọn đáp án B
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA=a\(\sqrt{2}\)
a) CMR các mặt bên của hình chóp là những tam giác vuông.
b) CMR (SAC) vuông góc với (SBD)
c)Tính góc giữa SC và mp (SAB)
d)Tính góc giữa hai mp(SBD) và (ABCD)
e)Tính khoảng cách giữa điểm A và mp (SCD).
a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)
tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)
ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)
Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)
b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)
c. Ta có : \(CB\perp\left(SAB\right)\) Hình chiếu vuông góc của SC lên (SAB) là SB nên góc giữa SC và (SAB) là \(\widehat{CSB}\)
Xét \(\Delta SAB\left(\perp A\right)\) ta có : Theo Pytago: \(SB^2=SA^2+AB^2\Leftrightarrow SB=\sqrt{2a^2+a^2}=a\sqrt{3}\)
Xét \(\Delta SBC\left(\perp B\right)\) ta có \(tan\widehat{CSB}=\frac{CB}{SB}=\frac{a}{a\sqrt{3}}\) \(\Rightarrow\widehat{BSC}=30^o\)