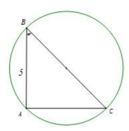
Cho tam giác ABC vuông tại A có A B = 5 , A B C = 30 o . Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là
A. 100 π 3
B. 200 π 3
C. 50 π 3
D. Kết quả khác
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Cho tam giác ABC vuông tại A có góc B=60 °. Tia phân giác của góc ABCcho tam giác abc vuông tại a có góc b = 60 độ . tia phân giác của góc b cắt ac tại e , kẻ eh vuông góc đc tại h a) chứng minh tam giác abe = tam giác hbe b) hb=hc C) từ H kẻ đường thẳng song song với BE cắt AC ở K .c/m🔺AHK là tam giác đều d) gọi I là giao điểm của BA và HE. Chúng minh IE>EH
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH
Câu 1. Tam giác ABC cân tại B có
0 B 40 thì A bằng:
A) 400 B) 70
0 C) 60
0 D) 50
0
Câu 2. Tam giác AED có AD2 = DE2 - AE2thì tam giác AEDA) vuông tại E B) vuông tại D C) vuông tại A D) không vuôngCâu 3. Cho tam giác ABC và tam giác có ba đỉnh D; E; F, biết AB = EF, B =F . Cần thêm điềukiện gì để hai tam giác bằng nhau theo trường hợp: góc - cạnh - góc?A) AC = FD B) A =F C) C=E D) A=ECâu 4. Cho tam giác DEF vuông cân tại D, có DE=3cm thì EF bằng:A) 18cm B) 12cm C) 12 cm D) 18 cm
II. BÀI TẬP TỰ LUẬN (8 điểm)Cho tam giác ABC có
0 A 90 và AB < BC. Gọi M là trung điểm của AC, trên tia đối của tia MB
lấy điểm D sao cho MD = MB. 1) Chứng minh ABM = CDM từ đó chứng minh AB=CD và AB //
Câu 1: B
Câu 2:Sửa đề: \(AD^2=DE^2+AE^2\)
=> Chọn A
Câu 3: Chọn D
Câu 4: \(EF=3\sqrt{2}cm\)
Cho tam giác ABC vuông tại A có góc B=60 độ.Trên cạnh Bc lấy điểm D sao cho BA=BD.Tia phân giác góc B cắt BC tại I
a)C/m tam giác BAD đều
b)C/m tam giác IBC cân
c)C/m D là trung điểm của BC
d) Cho tam giác ABC vuông tại A có BC=26 cm.Tính độ dàu AB và AC biết rằng AB:AC=5:2
(Bạn tự vẽ hình giùm)
a/ Ta có BA = BD (gt)
nên \(\Delta BAD\)cân tại B
=> \(\widehat{BAD}=\frac{180^o-\widehat{B}}{2}\)
=> \(\widehat{BAD}=\frac{180^o-60^o}{2}\)
=> \(\widehat{BAD}=\widehat{BDA}=60^o=\widehat{B}\)
=> \(\Delta BAD\)đều (đpcm)
b/ \(\Delta ABI\)và \(\Delta DBI\)có: AB = DB (gt)
\(\widehat{ABI}=\widehat{IBD}\)(BI là tia phân giác \(\widehat{B}\))
Cạnh BI chung
=> \(\Delta ABI\)= \(\Delta DBI\)(c. g. c) => \(\widehat{A}=\widehat{BDI}=90^o\)(hai cạnh tương ứng)
và AI = DI (hai cạnh tương ứng)
=> BI = IC (quan hệ giữa đường xiên và hình chiếu)
nên \(\Delta BIC\)cân tại I (đpcm)
c/ Ta có \(\Delta BIC\)cân tại I (cmt)
=> Đường cao ID cũng là đường trung tuyến của \(\Delta BIC\)
=> D là trung điểm BC (đpcm)
d/ Ta có \(\Delta ABC\)vuông tại A
=> BC2 = AB2 + AC2 (định lý Pythagore)
=> AB2 + AC2 = 262 = 676
và \(\frac{AB}{AC}=\frac{5}{2}\)=> \(\frac{AB}{5}=\frac{AC}{2}\)=> \(\frac{AB^2}{25}=\frac{AC^2}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{AB^2}{25}=\frac{AC^2}{4}=\frac{AB^2+AC^2}{25+4}=\frac{676}{29}\)
=> \(\hept{\begin{cases}\frac{AB}{5}=\frac{676}{29}\\\frac{AC}{2}=\frac{676}{29}\end{cases}}\)=> \(\hept{\begin{cases}AB=\frac{676}{29}.5\\AC=\frac{676}{29}.2\end{cases}}\)=> \(\hept{\begin{cases}AB=\frac{3380}{29}\left(cm\right)\\AC=\frac{1352}{29}\left(cm\right)\end{cases}}\)
Cho tam giác ABC vuông tại C. Ta có: 5.A=4.B. Tính góc A; góc B?
Vì tổng ba góc của tam giác bằng 180° nên tổng số đo của góc A và B bằng 90° mà 5A=4B nên => A =4/5 của B còn lại tính tổng tỉ
Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = c. Giải tam giác ABC, biết:
a, b = 5,4cm, C ^ = 30 0
b, c = 10cm, C ^ = 45 0
. Tam giác ABC có BC = 3cm ; AC = 5cm ; AB = 4cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C C. Tại A
D. Không phải là tam giác vuông
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
a) Tam giác ABC nhọn:
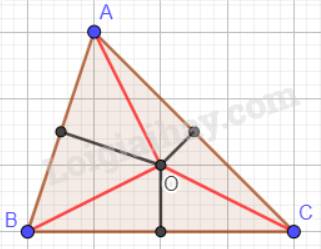
b) Tam giác ABC vuông tại A:
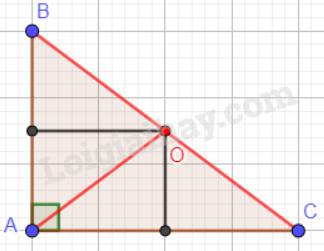
c) Tam giác ABC có góc A tù:
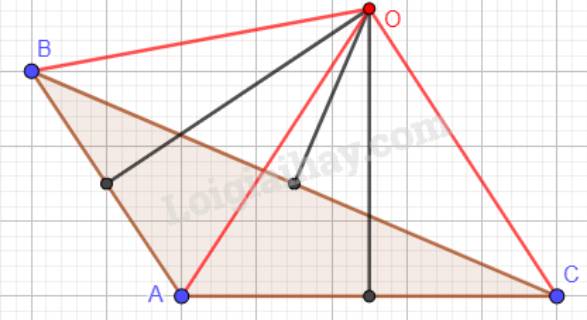
1.Cho tam giác ABC có A + B = C + 90 và A = C + 10. Tính các góc của tam giác ABC
2.Cho tam giác ABC vuông tại A, vẽ các tia phân giác của B và C cắt nhau tại M. Tính BMC
3.Cho tam giác ABC có A =80, B = 60. Hai tia phân giác của B và c cắt nhau tại I, vẽ tia p/g góc ngoài tại B sao cho B cắt tia CI tại D
a) Tính BIC
b)CMR BDC = C
1, Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc tam giác)
\(\Leftrightarrow\widehat{C}+90^o+\widehat{C}=180^o\)
\(\Leftrightarrow2\widehat{C}=90^o\)
\(\Leftrightarrow\widehat{C}=45^o\)
\(\Rightarrow\widehat{A}=\widehat{C}+10=55^o\)
\(\Rightarrow\widehat{B}=180^o-\widehat{A}-\widehat{C}=180^o-55^o-45^o=80^o\)
2,
Vì tam giác ABC vuông tại A
=> ^B + ^C = 90o
Vì BM là phân giác ^ABC
=>^B1 = \(\frac{\widehat{ABC}}{2}\)
Tương tự ^C1 = \(\frac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{90^o}{2}=45^o\)
Theo tổng 3 góc trong tam giác \(\widehat{BMC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-45^o=135^o\)
Cho tam giác ABC vuông tại A có góc B= 50 độ nội tiếp (O,4cm) . Vẽ dây AD vuông AB tại I
a) C/m ba điểm B , I , C thẳng hàng
b) Giải tam giác vuông ABC
c) C/m IB.IC=IA.ID
a: Sửa đề: vẽ dây AD vuông góc với đường kính của (O) tại I
ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
=>BC là đường kính của (O)
mà AD vuông góc với đường kính của (O)
nên AD\(\perp\)BC tại I
=>B,I,C thẳng hàng
b: BC=2*OB=8cm
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-50^0=40^0\)
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{8}=sin40\)
=>\(AB\simeq5,14\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{8^2-5.14^2}\simeq6,13\left(cm\right)\)
c: ΔOAD cân tại O
mà OI là đường cao
nên I là trung điểm của AD
ΔABC vuông tại A có AI là đường cao
nên \(AI^2=IB\cdot IC\)
=>\(IB\cdot IC=IA\cdot ID\)