tham khảo:

a)\(y'=xsin2x+sin^2x\)

\(y'=sin^2x+xsin2x\)

b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)

c)\(y=sin3x-3sinx\)

\(y'=3cos3x-3cosx\)

d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)

\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)

a: \(y'=\left(sin3x\right)'+\left(sin^2x\right)'=3\cdot cos3x+sin\left(x+pi\right)\)

b: \(y'=\left(log_2\left(2x+1\right)\right)'+\left(3^{-2x+1}\right)'\)

\(=\dfrac{2}{\left(2n+1\right)\cdot ln2}-2\cdot3^{-2x+1}\cdot ln3\)

Chọn A

Đáp án C

Ta có y ' = 1 - 2 cos   2 x ⇒ y ' = 0 ⇔ cos   2 x = 1 2 ⇒ x = ± π 6 + k π  hơn nữa y '  đổi dấu từ dương sang âm qua điểm - π 6  nên x = - π 6  là điểm cực tiểu của hàm số. (Ta có thể tính y ' ' = 4   s in 2 x ⇒ y ' ' ( π 6 ) < 0 ⇒ - π 6  là điểm cực đại của hàm số)

+ Xét hàm số  y= f(x) = cos3x

TXĐ: D =R

Với mọi x ∈ D , ta có: - x ∈ D  và

   f( -x) = cos( - 3x) = cos3x = f(x)

Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.

+ Xét hàm y= g(x)= sin(x² + 1)

TXĐ: D= R

Với mọi x ∈ D , ta có: - x ∈ D  và

 g( -x)= sin[ (-x)² +1]= sin( x²+1)= g(x)

    Do đó: y= sin( x² +1)  là hàm chẵn trên R.

    + Xét hàm số y= h( x)= tan²x .

    TXĐ: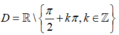 

Với mọi x ∈ D , ta có: - x ∈ D  và

    h( -x)= tan² (-x)= (- tanx)² = tan² x=  h(x)

Do đó y= tan²x là hàm số chẵn trên D.

+ Xét hàm số y= t(x)= cotx.

    TXĐ:  

Với mọi x ∈ D , ta có: - x ∈ D  và t(-x)= cot(-x) = - cotx = - t(x)

Do đó:  y= cotx là hàm số lẻ trên D.

Vậy (1); (2); (3) là các hàm số chẵn

Đáp án C

a.

\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)

b.

\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)

c.

\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)

\(a,y'=\left(f\left(g\left(x\right)\right)\right)'\)

\(=f'\left(g\left(x\right)\right).g'\left(x\right)\)

\(=e^{g\left(x\right)}.\left(2x-1\right)\)

\(=e^{x^2-x}.\left(2x-1\right)\)

\(b,y'=\dfrac{d}{dx}\left(3^{sinx}\right)\)

\(=\dfrac{d}{dx}\left(e^{ln3.sinx}\right)\)

\(=\dfrac{d}{dx}\left(ln3.sinx\right).e^{ln3.sinx}\)

\(=ln3.cosx.3^{sinx}\)

Đặt \(sinx=t\Rightarrow t\in\left[-\dfrac{1}{2};1\right]\)

\(y=f\left(t\right)=2t^2+t+4\)

Xét hàm \(f\left(t\right)=2t^2+t+4\) trên \(\left[-\dfrac{1}{2};1\right]\)

\(-\dfrac{b}{2a}=-\dfrac{1}{4}\in\left[-\dfrac{1}{2};1\right]\)

\(f\left(-\dfrac{1}{2}\right)=4\) ; \(f\left(-\dfrac{1}{4}\right)=\dfrac{31}{8}\); \(f\left(1\right)=7\)

\(y_{max}=7\) khi \(t=1\) hay \(x=\dfrac{\pi}{2}\)

\(y_{min}=\dfrac{31}{8}\) khi \(sinx=-\dfrac{1}{4}\)