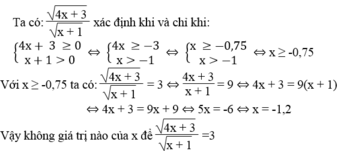\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|=5x\left(1\right)\)

Ta có :

\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|\ge\left|x+1+x+2+x+3+x+4\right|=\left|4x+10\right|\)

\(pt\left(1\right)\Leftrightarrow\left|4x+10\right|=5x\)

\(\Leftrightarrow\left[{}\begin{matrix}4x+10=5x\\4x+10=-5x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=10\\9x=-10\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-\dfrac{10}{9}\end{matrix}\right.\) \(\left(thỏa.mãnx\inℚ\right)\)

Lời giải:

Ta có:\(y^2+2\sqrt{2020}y+2022=(y^2+2\sqrt{2020}y+2020)+2=(y+\sqrt{2020})^2+2\geq 2(1)\)

Áp dụng BĐT Bunhiacopxky:

$(\sqrt{x-1}+\sqrt{3-x})^2\leq (x-1+3-x)(1+1)=4$

$\Rightarrow \sqrt{x-1}+\sqrt{3-x}\leq 2(2)$

Từ $(1); (2)\Rightarrow \sqrt{x-1}+\sqrt{3-x}\leq 2\leq y^2+2\sqrt{2020}y+2022$

Dấu "=" xảy ra khi mà: \(\left\{\begin{matrix} \frac{x-1}{1}=\frac{3-x}{1}\\ y+\sqrt{2020}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=2\\ y=-\sqrt{2020}\end{matrix}\right.\)

\(\left(\sqrt{x-1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(x-1+3-x\right)=4\\ \Leftrightarrow\sqrt{x-1}+\sqrt{3-x}\le2\\ y^2+2\sqrt{2020}y+2022=\left(y^2+2y\sqrt{2020}+2020\right)+2\\ =\left(y+\sqrt{2020}\right)^2+2\ge2\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-1=3-x\\y+\sqrt{2020}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\sqrt{2020}\end{matrix}\right.\)

Vậy ...

ĐKXĐ: \(3\ge x\ge1\)

Áp dụng BĐT Bunhiacopski:

\(1\sqrt{x-1}+1\sqrt{3-x}\le\sqrt{\left(1^2+1^2\right)\left(x-1+3-x\right)}=\sqrt{2.2}=2\)

Mặt khác: \(y^2+2\sqrt{2020}y+2022=\left(y+\sqrt{2020}\right)^2+2\ge2\)

Nên để thõa mãn yêu cầu bài toán thì

\(\left\{{}\begin{matrix}\sqrt{x-1}=\sqrt{3-x}\\y+\sqrt{2020}=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\left(tm\right)\\y=-\sqrt{2020}\end{matrix}\right.\)

`Answer:`

`1/5+2/7-1<x<\frac{13}{3}+6/5+\frac{4}{15}`

`VT =1/5+2/7-1=\frac{17}{35}-1=\frac{-18}{35}`

`VP=\frac{13}{3}+6/5+\frac{4}{15}=\frac{83}{15}+\frac{4}{15}=\frac{203}{35}`

`=>\frac{-18}{35}<x<\frac{203}{35}`

`=>-18<x<203`

Vậy `-18<x<203` với `x\inZZ`

\(\dfrac{1}{5}+\dfrac{2}{7}-1< x< \dfrac{13}{3}+\dfrac{6}{5}+\dfrac{4}{15}\)

\(\Leftrightarrow\dfrac{7}{35}+\dfrac{10}{35}-\dfrac{35}{35}< x< \dfrac{65}{15}+\dfrac{18}{15}+\dfrac{4}{15}\)

\(\Leftrightarrow\dfrac{-18}{35}< x< \dfrac{29}{5}\)

\(\Leftrightarrow\dfrac{-18}{35}< \dfrac{35x}{35}< \dfrac{203}{35}\)

\(\Leftrightarrow-18< 35x< 203\)

\(\Leftrightarrow x\in\left\{0;1;2;3;4;5\right\}\)

mình ko hiểu

<=> (x-2)(x+y-2)=3

=>\(\hept{\begin{cases}x-2=1\\x+y-2=3\end{cases};\hept{\begin{cases}x-2=-1\\x+y-2=-3\end{cases};\hept{\begin{cases}x-2=3\\x+y-2=1\end{cases};\hept{\begin{cases}x-2=-3\\x+y-2=-1\end{cases}}}}}\)

=> \(\hept{\begin{cases}x=3\\y=2\end{cases};\hept{\begin{cases}x=1\\y=-2\end{cases};\hept{\begin{cases}x=5\\y=-2\end{cases};\hept{\begin{cases}x=-1\\y=2\end{cases}}}}}\)