Tổng tất cả các giá trị m để phương trình x 4 - 2 m + 1 x 2 + 2 m + 1 = 0 (1) có bốn nghiệm phân biệt lập thành cấp số cộng
A . 14 9
B . 32 9
C . 17 3
D . 19 3
Câu 1: Tìm tất cả các giá trị cuả tham số m để phương trình \(4\sqrt{x^2-4x+5} =x^2-4x+2m-1\) có 4 nghiệm phân biệt
Câu 2: Tìm các giá trị của tham số m sao cho tổng các bình phương hai nghiệm của phương trình \((m-3)x^2+2x-4=0\) bằng 4
Câu 3: Cho tam giác ABC có \(BC=a, AC=b, AB=c\) và I là tâm đường tròn nội tiếp tam giác. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\)
Câu 4: Cho tam giác ABC. Gọi D,I lần lượt là các điểm xác định bởi \(3\overrightarrow{BD}-\overrightarrow{BC}=\overrightarrow{0}\) và \(\overrightarrow{IA}+\overrightarrow{ID}=\overrightarrow{0}\). Gọi M là điểm thỏa mãn \(\overrightarrow{AM}=x\overrightarrow{AC}\) (x∈R)
a) Biểu thị \(\overrightarrow{BI}\) theo \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\)
b) Tìm x để ba điểm B,I,M thẳng hàng
1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)
3.
Nối AI kéo dài cắt BC tại D thì D là chân đường vuông góc của đỉnh A trên BC
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{c}{b}\)
\(\Rightarrow\overrightarrow{BD}=\dfrac{c}{b}\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{ID}-\overrightarrow{IB}=\dfrac{c}{b}\left(\overrightarrow{IC}-\overrightarrow{ID}\right)\)
\(\Leftrightarrow b.\overrightarrow{IB}+\overrightarrow{c}.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}\) (1)
Mặt khác:
\(\dfrac{ID}{IA}=\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{a}{b+c}\)
\(\Leftrightarrow\left(b+c\right)\overrightarrow{ID}=-a.\overrightarrow{IA}\) (2)
(1); (2) \(\Rightarrow a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}-\left(b+c\right)\overrightarrow{ID}=\overrightarrow{0}\)
Câu 1: Gọi M là tập hợp tất cả các giá trị nguyên của tham số m để phương trình \(-x^2+\left(2m-3\right)x-m^2+m+20=0\) có hai nhgieemj trái dấu. Tổng tất cả các phần tử của M bằng
A. 5 B. 4 C. 10 D. 15
Câu 2: Có tất cả bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2022 để bất phương trình \(x^2-8x+m+20\ge0\) nghiệm đúng với mọi x ϵ [5; 10]?
A. 2027 B. 2028 C. 2062 D. 2063
Tổng tất cả các giá trị nguyên của m để phương trình 4 sin x + ( m - 4 ) cos x - 2 m + 5 = 0 có nghiệm là:
A. 5
B. 6
C. 10
D. 3
cho phương trình \(x^2-2mx+m-4=0\) (1).Tìm tất cả các giá trị nguyên của m để phương trình (1) có 2 nghiệm nguyên
\(pt:x^2-2mx+m-4=0\left(1\right)\)
\(\Delta'=\left(-m\right)^2-\left(m-4\right)=m^2-m+4=m^2-2.\dfrac{1}{2}m+\dfrac{1}{4}-\dfrac{1}{4}+4\)
\(=\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{6}>0\left(\forall m\right)\)
=> \(pt\left(1\right)\) luôn có 2 nghiệm phân biệt x1,x2 \(\forall m\)
\(Theo\) \(\)Vi ét\(=>\left\{{}\begin{matrix}x1+x2=2m\left(1\right)\\x1x2=m-4\left(2\right)\end{matrix}\right.\)
từ(1)
với \(x1x2=m-4=>m=x1x2+4\)
thay \(m=x1x2+4\) vào (1)\(\)\(=>x1+x2=2\left(x1x2+4\right)\)
\(< =>x1+x2=2x1x2+8\)
\(< =>x1+x2-2x1x2=8\)
\(< =>2x1+2x2-4x1x2=16\)
\(=>2x1\left(1-2x2\right)-\left(1-2x2\right)=15\)
\(< =>\left(2x1-1\right)\left(1-2x2\right)=16\)(3)
để (3) nguyên \(< =>\left(2x1-1\right)\left(1-2x2\right)\inƯ\left(16\right)=\left\{\pm1;\pm2;\pm4;\pm8;\pm16\right\}\)
đến đây bạn tự lập bảng giá trị để tìm x1,x2 rồi từ đó thay thế x1,x2 vào(2) để tìm m nhé (mik ko làm nữa dài lắm)
Cho phương trình : \(x^4-2\left(m+1\right)x^2+m^2+m+2=0\) tìm tất cả các giá trị của m để phương trình có bốn nghiệm phân biệt lớn hơn -1
Tìm tất cả các giá trị thực của m để phương trình \(4^x-2^{x+1}+m=0\) có 2 nghiệm thực phân biệt
Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-2t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương: \(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1-m>0\\2>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)
Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình m 2 x 4 - 16 + m x 2 - 4 - 28 x - 2 ≥ 0 đúng với mọi x ∈ R . Tổng giá trị của tất cả các phần tử thuộc S bằng
A. - 15 8
B. - 1
C. - 1 8
D. 7 8
Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình m2(x4 - 1) + m(x2 - 1) - 6(x - 1) ≥ 0 đúng với mọi x ∈ R. Tổng giá trị của tất cả các phần tử thuộc S bằng bao nhiêu ?
Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$
Cho phương trình \(x^2-2\left(m+1\right)x+m^2-1=0\). Tìm tất cả các giá trị của m để phương trình có nghiệm
phương trình có nghiệm khi:
\(\Delta\)\(\ge\)0<=>[-(2m+1)]^2-4.(m^2-1)\(\ge\)0
<=>(2m+2)^2-4m^2+4\(\ge\)0
<=>4m^2+8m+4-4m^2+4\(\ge\)0
<=>8m+8\(\ge\)0
<=>8(m+1)\(\ge\)0
<=>m\(\ge\)-1
vậy m\(\ge\)-1 thì phương trình có nghiệm
△≥0⇔(2m+2)^2-4(m^2-1)≥0
⇔4m^2+8m+4-4m^2+4≥0
⇔8m+8≥0
⇔m≥-1
Vậy phương trình có nghiệm khi m≥-1
Tìm tổng tất cả các giá trị nguyên của m để phương trình 4 1 + x + 4 1 - x = ( m + 1 ) ( 2 2 + x - 2 2 - x ) + 16 - 8 m có nghiệm trên 0 ; 1
A. 2.
B. 5.
C. 4.
D. 3.
Đáp án D.
Phương trình tương đương với

Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
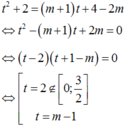
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.