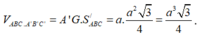Cho lăng trụ tam giác A B C . A ' B ' C ' . Mặt phẳng đi qua A, B và trung điểm M của cạnh C C ' chia lăng trụ thành 2 phần có thể tích V 1 , V 2 V 1 > V 2 . Tỉ số V 1 V 2 là
A. 4
B. 2
C. 5
D. 3
Bài tập : Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A , AB = a , BC = a\(\sqrt{3}\) và mặt phẳng (A'BC) tạo với mặt phẳng đáy một góc 600 . Tính V khối lăng trụ đã cho .
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60 0 , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A′B′C′ là
A. 3 3 4
B. 3
C. 3
D. 3 3
Cho hình lăng trụ đứng ABC.A' B' C' có đáy là tam giác vuông cân đỉnh A, BC=2a, thể tích khối lăng trụ đã cho bằng a 3 . Khoảng cách từ điểm B' đến mặt phẳng (A' BC) bằng
A. 2 a B. 6 a 4 . C. 2 a 2 . D. 6 a 3
B. 6 a 4 .
C. 2 a 2 .
Cho lăng trụ tam giác ABC.A' B' C' có đáy là tam giác vuông cân tại A,AA' = a 3 hình chiếu vuông góc của A’ lên (ABC) là trung điểm cạnh AC. Biết góc giữa AA' và mặt phẳng (ABC) bằng 45 0 . Thể tích của khối lăng trụ ABC.A' B' C' là:
A. a 3 6
B. a 3 3 4
C. 3 a 3 6 2
D. a 3 6 3
Cho hình lăng trụ đều ABC.A¢B¢C¢. Biết mặt phẳng (A'BC) tạo với mặt phẳng (ABC) một góc 30 0 và tam giác có A'BC diện tích bằng 8a2. Tính thể tích khối lăng trụ ABC.A¢B¢C¢.
A. 8 a 3 3
B. 8 a 3
C. 8 a 3 3 3
D. 8 a 3 3
Cho lăng trụ tam giác ABC.A'B'C'. Mặt phẳng đi qua A,B và trung điểm M của cạnh ![]() chia lăng trụ thành 2 phần có thể tích
V
1
,
V
2
V
1
>
V
2
. Tỉ số
V
1
V
2
là
chia lăng trụ thành 2 phần có thể tích
V
1
,
V
2
V
1
>
V
2
. Tỉ số
V
1
V
2
là
A. 4
B. 2
C. 5
D. 3
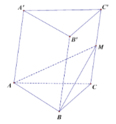
Hình chóp MABC có cùng diện tích đáy với hình lăng trụ
Và có chiều cao bằng 2 lăng trụ nên
V 2 = 1 6 V ABC . A ' B ' C ' ⇒ V 1 = 5 6 V ABC . A ' B ' C ' ⇒ V 1 V 2 = 5
Đáp án cần chọn là C
Cho hình lăng trụ tứ giác ABCD. A’B’C’D’. Một mặt phẳng song song với mặt phẳng (A’B’C’D’) cắt các cạnh bên của hình lăng trụ lần lượt tại A”, B”, C”, D”. Hỏi hình tạo bởi các điểm A, B, C, D, A”, B”, C”, D” là hình gì?
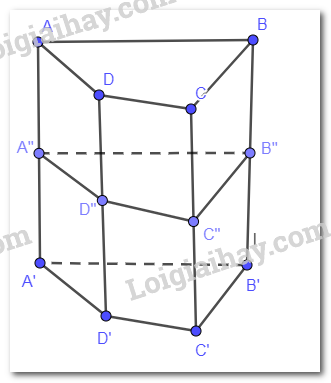
Mặt phẳng (ABCD) song song với (A"B"C"D") (do cùng song song với (A'B'C'D')) nên ABCD.A"B"C"D" là hình lăng trụ tứ giác.
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A′ xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC′A′) tạo với đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A′B′C′.
A. 3 a 3 2
B. 3 a 3 3 2
C. a 3 3 2
D. a 3 3 3
Đáp án B
Gọi M, N lần lượt là trung điểm của AC và AM.
Khi đó ΔAHM là tam giác đều và NH ⊥ AC .


Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều ba điểm A, B, C. Cạnh bên AA’ tạo với mặt phẳng đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A’B’C’
A . a 3 3 10
B . a 3 3 12
C . a 3 3 4
D . a 3 3 8
Cho khối lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C. Cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC.A'B'C' là:
A. a 3 3
B. a 3 3 2
C. a 3 3 6
D. a 3 3 4
Chọn đáp án D.
Ta có A'A = A'B = A'C nên hình chiếu của A' là tâm đường tròn ngoại tiếp tam giác ABC.
Do tam giác ABC đều nên trọng tâm G là tâm đường tròn ngoại tiếp tam giác ABC.
![]()
AG là hình chiếu của A'A lên mặt phẳng (ABC)
Góc giữa A'A với mặt phẳng (ABC) là: A ' A G ^
Gọi H là trung điểm BC.
Ta có: 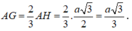
Xét tam giác A'AG vuông tại G:
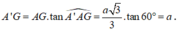
Diện tích tam giác đều ABC là:
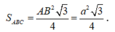
Thể tích khối lăng trụ ABC.A'B'C' là: