Cho hình chóp S.ABCD có đáy là hình bình hành, cạnh bên SA vuông góc
Những câu hỏi liên quan
1) cho hình chóp S.MNPQ có đáy là hình vuông cạnh bên SM vuông góc với đáy. Góc giữa 2 đường thẳng SM và PQ là2) cho hình chóp S.ABCD có đáy là hình bình hành cạnh bên SA vuông góc với đáy. Góc giữa 2 đường thẳng SC và AB là3) cho hình chóp tam giác S.ABC có SA vuông góc với đáy. H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúngA. BC vuông ABB. SH vuông ACC. BC vuông AHD. SB vuông SA
Đọc tiếp
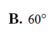
1) cho hình chóp S.MNPQ có đáy là hình vuông cạnh bên SM vuông góc với đáy. Góc giữa 2 đường thẳng SM và PQ là
2) cho hình chóp S.ABCD có đáy là hình bình hành cạnh bên SA vuông góc với đáy. Góc giữa 2 đường thẳng SC và AB là
3) cho hình chóp tam giác S.ABC có SA vuông góc với đáy. H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúng
A. BC vuông AB
B. SH vuông AC
C. BC vuông AH
D. SB vuông SA
Câu 1:
SM\(\perp\)(MNPQ)
=>SM\(\perp\)PQ
=>\(\widehat{SM;PQ}=90^0\)
Câu 3: C
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
3
a
,
A
D
4
a
,
B
A
D
^
120
0
. Cạnh bên SA vuông góc với đáy và
S
A
2
a
3
. Tính góc giữa hai mặt phẳng...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = 3 a , A D = 4 a , B A D ^ = 120 0 . Cạnh bên SA vuông góc với đáy và S A = 2 a 3 . Tính góc giữa hai mặt phẳng S B C và S C D
A. 45 0
B. arccos 17 2 26
C. 60 °
D. 30 °
Đáp án A
Dựng trục tọa độ với A 0 ; 0 ; 0 ; 0 ; 4 a ; 0 ; S 0 ; 0 ; 2 a 3
Ta có: A H = A B sin 60 0 = 3 a 3 2 ; B H = 3 a 2
Do đó B = 3 a 3 2 ; − 3 a 2 ; 0 ; C 3 a 3 2 ; 5 a 2 ; 0
Khi đó n S B C ¯ = k S B ¯ ; B C ¯ = 4 ; 0 ; 3 ; n S C D ¯ = k S C ¯ ; D C ¯ = 3 ; 3 ; 2 3
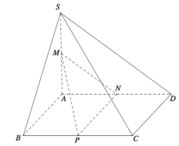
Do đó cos S B C ; S C D ^ = 10 3 4 2 + 3 2 24 = 1 2 ⇒ S B C ; S C D ^ = 45 0
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SC tạo với đáy góc
60
ο
. Thể tích khối chóp S.ABCD là: A.
a
3
6
3
B.
a
3
3
6
C. ...
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SC tạo với đáy góc 60 ο . Thể tích khối chóp S.ABCD là:
A. a 3 6 3
B. a 3 3 6
C. a 3 6 6
D. a 3 3 3
Cho hình chóp S.ABCD có đáy là hình bình hành, cạnh bên SA vuông góc với đáy. Biết khoảng cách từ A đến (SBD) bằng
6
a
7
. Tính khoảng cách từ C đến mặt phẳng (SBD)?
Đọc tiếp
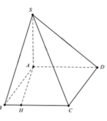
Cho hình chóp S.ABCD có đáy là hình bình hành, cạnh bên SA vuông góc với đáy. Biết khoảng cách từ A đến (SBD) bằng 6 a 7 . Tính khoảng cách từ C đến mặt phẳng (SBD)?
Cho hình chóp S.ABCD có đáy là hình bình hành, cạnh bên SA vuông góc với đáy. Biết khoảng cách từ A đến (SBD) bằng
6
a
7
.
Tính khoảng cách từ C đến mặt phẳng (SBD)? A.
12
a
7
B.
3
a
7
C.
4...
Đọc tiếp
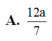
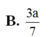
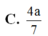
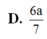
Cho hình chóp S.ABCD có đáy là hình bình hành, cạnh bên SA vuông góc với đáy. Biết khoảng cách từ A đến (SBD) bằng 6 a 7 . Tính khoảng cách từ C đến mặt phẳng (SBD)?
A. 12 a 7
B. 3 a 7
C. 4 a 7
D. 6 a 7
Cho khối chóp S.ABCD có đáy là hình bình hành, AB3, AD4,
B
A
D
^
120
0
. Cạnh bên SA
2
3
vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP). A. 60
°
B. 45
°
C. 90
°
D. 30...
Đọc tiếp
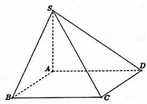
Cho khối chóp S.ABCD có đáy là hình bình hành, AB=3, AD=4, B A D ^ = 120 0 . Cạnh bên SA = 2 3 vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP).
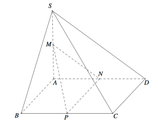
A. 60 °
B. 45 °
C. 90 °
D. 30 °
Cho khối chóp S.ABCD có đáy là hình bình hành, AB3, AD4,
B
A
D
^
120
o
Cạnh bên SA
2
3
vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳn...
Đọc tiếp
Cho khối chóp S.ABCD có đáy là hình bình hành, AB=3, AD=4, B A D ^ = 120 o Cạnh bên SA= 2 3 vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP).
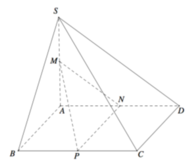
A. 60 o
B. 45 o
C. 90 o
D. 30 o
Đáp án B
Ta có
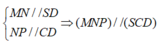
Tính được
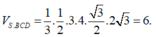
Ta có
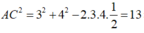
Tam giác SBC có
Tam giác
Vì vậy
Đúng 0
Bình luận (0)
Cho khối chóp S.ABCD có đáy là hình bình hành,
A
B
3
,
A
D
4
,
B
A
D
^
120
°
Cạnh bên
S
A
2
3
vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳ...
Đọc tiếp
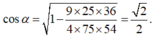
Cho khối chóp S.ABCD có đáy là hình bình hành, A B = 3 , A D = 4 , B A D ^ = 120 ° Cạnh bên S A = 2 3 vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP).
A. 60 °
B. 45 °
C. 90 °
D. 30 °
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặtphẳng đáy và
S
A
a
2
. Thể tích của khối chóp S.ABCD là A.
a
3
2
6
B.
a
3
2
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt
phẳng đáy và S A = a 2 . Thể tích của khối chóp S.ABCD là
A. a 3 2 6
B. a 3 2
C. a 3 2 4
D. a 3 2 3
