Cho tam giác ABC, đường cao AH, Gọi M là trung điểm của AC Lấy D đối xứng với H qua M. Chứng minh tứ giác AHCD là hình chữ nhật
Những câu hỏi liên quan
5 tháng 11 2023 lúc 21:27
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy D là điểm đối xứng với H qua I. Chứng minh tứ giác AHCD là hình chữ nhật.
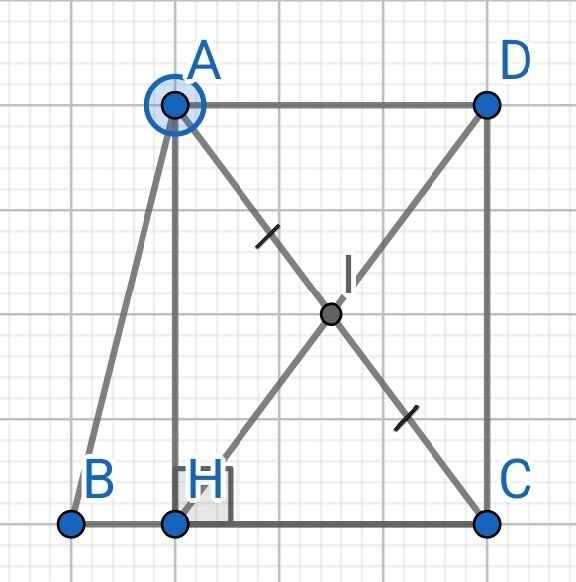Do D và H đối xứng nhau qua I (gt)
⇒ I là trung điểm của DH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ ∠AHC = 90⁰
Tứ giác AHCD có:
I là trung điểm của AC (gt)
I là trung điểm của DH (cmt)
⇒ AHCD là hình bình hành
Mà ∠AHC = 90⁰ (cmt)
⇒ AHCD là hình chữ nhật
Đúng 1
Bình luận (0)
Bài 1. Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC . Lấy D là điểm đối xứng với H qua I . Chứng minh tứ giác AHCD là hình chữ nhật
Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
Đúng 2
Bình luận (0)
+)Xét tứ giác AHCD có :
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
+)Hình bình hành AHCD có góc AHC = 90độ
=> AHCD là hình chữ nhật
Đúng 0
Bình luận (0)
cho tam giác abc đường cao ah gọi i là trung điểm của ac. lấy D là điểm đối xứng với H qua I. chứng minh tam giác AHCD là hình chữ nhật
Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
Do đó: AHCD là hình bình hành
Hình bình hành AHCD có\(\widehat{AHC}=90^0\)
nen AHCD là hình chữ nhật
Đúng 0
Bình luận (0)
1. Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC . Lấy D là điểm đối xứng vớiH qua I . Chứng minh tứ giác AHCD là hình chữ nhật.2. Cho tam giác ABC vuông tại A, đường cao AH . Gọi I , K theo thứ tự là trung điểm của AB ,AC . Chứng minh:a) IHK � 90� � ; b) Chu vi �IHK bằng nửa chu vi �ABC .3. Tìm x trong hình vẽ bên, Biết AB �13 cm, BC �15 cm, AD �10cm.4. Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E , F , G , H theo thứ tự làtrung điểm của các cạnh AB , BC , CD, DA...
Đọc tiếp
1. Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC . Lấy D là điểm đối xứng với
H qua I . Chứng minh tứ giác AHCD là hình chữ nhật.
2. Cho tam giác ABC vuông tại A, đường cao AH . Gọi I , K theo thứ tự là trung điểm của AB ,
AC . Chứng minh:
a) IHK � 90� � ; b) Chu vi �IHK bằng nửa chu vi �ABC .
3. Tìm x trong hình vẽ bên, Biết AB �13 cm, BC �15 cm, AD �10
cm.
4. Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E , F , G , H theo thứ tự là
trung điểm của các cạnh AB , BC , CD, DA . Chứng minh tứ giác HEFG là hình chữ nhật.
5. Cho hình thang cân ABCD ( AB CD � , AB CD � ). Gọi M , N , P , Q lần lượt là trung điểm
các đoạn thẳng AD , BD , AC , BC .
a) Chứng minh bốn điểm M , N , P , Q thẳng hàng;
b) Chứng minh tứ giác ABPN là hình thang cân;
c) Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật.
6. Cho tam giác ABC có đường cao AI . Từ A kẻ tia Ax vuông góc với AC , từ B kẻ tia By
song song với AC . Gọi M là giao điểm của tia Ax và tia By . Nối M với trung điểm P của AB ,
đường MP cắt AC tại Q và BQ cắt AI tại H .
a) Tứ giác AMBQ là hình gì? b) Chứng minh tam giác PIQ cân.
7. Cho tam giác ABC . Gọi O là một điểm thuộc miền trong của tam giác. M ,
N , P , Q lần lượt là trung điểm của các đoạn thẳng OB , OC , AC , AB .
a) Chứng minh tứ giác MNPQ là hình bình hành;
b) Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật.
Bài 1:
Xét tứ giác AHCD có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo HD
Do đó: AHCD là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC đường cao AH M là trung điểm của AC D đối xứng với H qua M Chứng minh tam giác AHCD là hình chữ nhật
có:
M là trung điểm của AC (gt)
D đối xứng H qua M(gt) => M là trung điểm của DH
Xét tứ giác AHCD có:
2 đường chéo cắt nhau tại trung điểm mỗi đường(cmt)
=> Tứ giác AHCD là hình chữ nhật
Nhớ tick cho mình nha
Đúng 1
Bình luận (0)
Cho tan giác ABC vuông tại A , AC=2AB ,đường cao AH. Gọi M là trung điểm của AC. Vẽ MK vuông góc với BC tại K
a) Chứng minh tứ giác AHKM là hình thang vuông
b) Lấy điểm D đối xứng vói điểm H qua điểm M. Tứ giác AHCD là hình gì ?
c) Chứng minh tam giác AHK cân
Xem chi tiết
Cho tam giác ABC và đường cao AH . Gọi M,N lần lượt là trung điểm của AB,AC. Gọi D là điểm đối xứng với H qua M,E là điểm đối xứng với H qua N. Chứng minh rằng A) tứ giác AHBD là hình chữ nhật B) tứ giác AHCE là hình chữ nhật
cho tam giác ABC vuông tại A.Gọi M là trung điểm của cạnh AC.Vẽ AH là đường cao của tam giác ABC H thuộc BC , gọi D là điểm đối xứng với H qua M.a. Chứng minh tứ giác AHCD là hình chữ nhậtb. Trên tia đối của tia HA lấy điểm E sao cho HE HA Tứ giác HECD là hình gì vì sao c. Chứng minh HD vuông góc với BEd. Cho cạnh AH 3 cm AC 5cm Tính diện tích tứ giác AHCDe. Tính độ dài DE
CHỊU TỰ TÍNH NHA HỎI NGƯỜI NHÀ HOẶC TRA GOOGLE
cho tam giác ABC vuông tại A.Gọi M là trung điểm của cạnh AC.Vẽ AH là đường cao của tam giác ABC H thuộc BC , gọi D là điểm đối xứng với H qua M.a. Chứng minh tứ giác AHCD là hình chữ nhậtb. Trên tia đối của tia HA lấy điểm E sao cho HE HA Tứ giác HECD là hình gì vì sao c. Chứng minh HD vuông góc với BEd. Cho cạnh AH 3 cm AC 5cm Tính diện tích tứ giác AHCDe. Tính độ dài DE
ôi mình chịu thôi :((