Cho hai số phức z = - 2 + 5 i , z ’ = a + b i a , b ∈ R . Xác định a,b để z + z’ là một số thuần ảo
A. a = 2 , b = - 5
B. a ≠ 2 , b = - 5
C. a ≠ 2 , b ≠ - 5
D. a = 2 , b ≠ - 5
Những câu hỏi liên quan
Câu 1 : Cho số phức z thỏa mãn z + ( 2 - i )overline{z} 3 - 5i. Môđun của số phức w z - i bằng bao nhiêu ?Câu 2 : Cho số phức z a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )z + ( 2 - i )2 4 + i. Tính P a - b
Đọc tiếp
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z a + bi(a,b
∈
ℝ
) và xét hai số phức
α
z
2
+
(
z
¯
)
2
v
à
β
2
.
z
.
z
¯
+...
Đọc tiếp
Cho số phức z = a + bi(a,b ∈ ℝ ) và xét hai số phức α = z 2 + ( z ¯ ) 2 v à β = 2 . z . z ¯ + i . ( z - z ¯ ) . Trong các khẳng định dưới đây, khẳng định nào đúng?
A. α là số thực, β là số thực.
B. α là số ảo, β là số thực.
C. α là số thực, β là số ảo.
D. α là số ảo, β là số ảo.
∈
ℝ
Cho số phức za+bi (a,b ) và xét hai số phức
α
z
2
+
(
z
¯
)
2
v
à
β
2
z
.
z
¯
+
i
(
z
-
z
¯
)
. Trong...
Đọc tiếp
∈ ℝ Cho số phức z=a+bi (a,b ) và xét hai số phức α = z 2 + ( z ¯ ) 2 v à β = 2 z . z ¯ + i ( z - z ¯ ) . Trong các khẳng định dưới đây, khẳng định nào đúng?
Cho hai số phức
z
5
+
2
i
v
à
z
1
-
i
. Tính mô-đun của số phức
w
z
-...
Đọc tiếp
Cho hai số phức z = 5 + 2 i v à z ' = 1 - i . Tính mô-đun của số phức w = z - z '
A. 5.
B. 3 5
C. 17
D. 37
Chọn đáp án A
Ta có w = z - z ' = 4 + 3 i
⇒ w = 4 2 + 3 2 = 5
Đúng 0
Bình luận (0)
Cho hai số phức
z
5
+
2
i
và
z
1
-
i
. Tính mô-đun của số phức
w
z
-
z...
Đọc tiếp
Cho hai số phức z = 5 + 2 i và z ' = 1 - i . Tính mô-đun của số phức w = z - z '
A. 7(cm)
B. 3(cm)
C. 6(cm)
D. 2(cm)
Chọn đáp án B
Gọi các kích thước của khối hộp là a (cm), b(cm), c (cm) với a, b, c là các số nguyên dương.
Từ giả thiết ta có
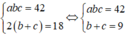
Lại có 9 = b + c ≥ 2 b c ⇒ b c ≤ 81 4
Mà b, c là các số nguyên dương nên b c ≤ 20
Từ b +c =9
⇒ trong hai số b, c có 1 số lẻ và 1 số chẵn ⇒ bc chẵn.
Từ a = 42 b c và a nguyên dương nên bc là ước nguyên dương của 42.
Nếu bc =6 thì b, c là nghiệm của phương trình X 2 - 9 X + 6 = 0 (loại vì nghiệm của phương trình này không là số nguyên).
Nếu bc =14 thì b, c là nghiệm của phương trình
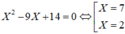
⇒ b c = 14 thỏa mãn. Vậy chiều cao của khối hộp là a = 42 b c = 3 c m
Đúng 0
Bình luận (0)
Cho hai số phức
z
1
7
+
9
i
và
z
2
8
i
. Gọi
z
a
+
b
i
a
,
b
∈
ℝ
là số phức thỏa mãn
z
−
1
−...
Đọc tiếp
Cho hai số phức z 1 = 7 + 9 i và z 2 = 8 i . Gọi z = a + b i a , b ∈ ℝ là số phức thỏa mãn z − 1 − i = 5 . Tìm a+b, biết biểu thức P = z − z 1 + 2 z − z 2 đạt giá trị nhỏ nhất.
A. ‒3
B. ‒7
C. 3
D. 7
Cho hai số phức
z
1
7
+
9
i
và
z
2
8
i
. Gọi
z
a
+
b
i
a
,
b
∈
ℝ
là số phức thỏa mãn
z
−
1
−...
Đọc tiếp
Cho hai số phức z 1 = 7 + 9 i và z 2 = 8 i . Gọi z = a + b i a , b ∈ ℝ là số phức thỏa mãn z − 1 − i = 5 . Tìm a + b , biết biểu thức P = z − z 1 + 2 z − z 2 đạt giá trị nhỏ nhất
A. ‒3
B. ‒7
C. 3
D. 7
Đáp án D.
Gọi M a ; b là điểm biểu diễn số phức z = a + b i . Đặt I = 1 ; 1 , A 7 ; 9 và B 0 ; 8
Ta xét bài toán: Tìm điểm M thuộc đường tròn C có tâm I, bán kính R = 5 sao cho biểu thức P = M A + 2 M B đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K x ; y sao cho M A = 2 M K ∀ M ∈ C .
Ta có
M A = 2 M K ⇔ M A 2 = 4 M K 2 ⇔ M I → + I A → 2 = 4 M I → + I K → 2
⇔ M I 2 + I A 2 + 2 M I → . I A → = 4 M I 2 + I K 2 + 2 M I → . I K →
⇔ 2 M I → I A → − 4 I K → = 3 R 2 + 4 I K 2 − I A 2 *
(*) luôn đúng ∀ M ∈ C ⇔ I A → − 4 I K → = 0 → 3 R 2 + 4 I K 2 − I A 2 = 0 .
I A → − 4 I K → = 0 → ⇔ 4 x − 1 = 6 4 y − 1 = 8 ⇔ x = 5 2 y = 3
Thử trực tiếp ta thấy K 5 2 ; 3 thỏa mãn 3 R 2 + 4 I K 2 − I A 2 = 0 .
Ta cos M A + 2 M B = 2 M K + 2 M B = 2 M K + M B ≥ 2 K B .
Vì B I 2 = 1 2 + 7 2 = 50 > R 2 = 25 nên B nằm ngoài (C).
Vì K I 2 = 3 2 2 + 2 2 < R 2 = 25 nên K nằm trong (C) .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK . Do đó M A + 2 M B nhỏ nhất khi và chỉ khi M là giao điểm của (C) và đường thẳng BK.
Phương trình đường thẳng B K : 2 x + y − 8 = 0 .
Phương trình đường tròn C : x − 1 2 + y − 1 2 = 25 .
Tọa độ điểm M là nghiệm của hệ
2 x + y = 8 x − 1 2 + y − 1 2 = 25 ⇔ x = 1 y = 6
hoặc x = 5 y = − 2 .
Thử lại thấy M 1 ; 6 thuộc đoạn BK.
Vậy a = 1, b = 6 ⇒ a + b = 7 .
Đúng 0
Bình luận (0)
Biết số phức z thỏa mãn đồng thời hai điều kiện
z
-
3
-
4
i
5
và biểu thức
M
|
z
+
2
|
2
-
|
z
-
i
|
2
đạt giá tri lớn nhất. Tính môđun của số phức z+i
Đọc tiếp
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
Cho số phức z thoả mãn đồng thời hai điều kiện
z
-
3
-
4
i
5
và biểu thức
M
z
+
2
2
-
z
-
i
2
đ...
Đọc tiếp
Cho số phức z thoả mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Môđun của số phức z - 2 - i bằng
A. 5
B. 9
C. 25
D. 5
Cho số phức z ( 2 + i)( 3 - i) Tìm phần thực a và phần ảo b của số phức
z
¯
A. a 7 ; b 1. B. a 7 ; b -1. C. a - 7; b 1. D. a -7; b - 1.
Đọc tiếp
Cho số phức z = ( 2 + i)( 3 - i) Tìm phần thực a và phần ảo b của số phức z ¯
A. a = 7 ; b = 1.
B. a = 7 ; b = -1.
C. a = - 7; b = 1.
D. a = -7; b = - 1.
Chọn B.
Ta có: z = ( 2 + i) ( 3 - i) = 6 - 2i + 3i - i2 = 7 + i
Nên 
vậy phần thực bằng a = 7 và phần ảo b = -1.
Đúng 0
Bình luận (0)