Các câu hỏi tương tự
∈
ℝ
Cho số phức za+bi (a,b ) và xét hai số phức
α
z
2
+
(
z
¯
)
2
v
à
β
2
z
.
z
¯
+
i
(
z
-
z
¯
)
. Trong...
Đọc tiếp
∈ ℝ Cho số phức z=a+bi (a,b ) và xét hai số phức α = z 2 + ( z ¯ ) 2 v à β = 2 z . z ¯ + i ( z - z ¯ ) . Trong các khẳng định dưới đây, khẳng định nào đúng?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai mặt phẳng
(
α
)
:
x
+
y
+
z
-
1
0
và
(
β
)
:
2
x
-
y
+
m
z
-
m
+
1
0
, với m là tham số thực. Giá trị của m để
(
α
)
⊥
(
β...
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng ( α ) : x + y + z - 1 = 0 và ( β ) : 2 x - y + m z - m + 1 = 0 , với m là tham số thực. Giá trị của m để ( α ) ⊥ ( β ) là
A. -1
B. 0
C. 1
D. -4
Trong không gian Oxyz, cho hai mặt phẳng
α
: x+y+z-10và
β
: 2x-y+mz-m+10, với m là tham số thực. Giá trị của m để
α
⊥
β
là A. -1 B. 0 C. 0 D. -4
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng α : x+y+z-1=0và β : 2x-y+mz-m+1=0, với m là tham số thực. Giá trị của m để α ⊥ β là
A. -1
B. 0
C. 0
D. -4
Cho các góc
α
,
β
và có số phức z cos
α
+ i.sin
β
. Khi đó x z.w thì:
A
.
x
cos
(
α
-
β
)
+
i
.
sin
(
α
+
β
)
B
.
x
cos
(
α...
Đọc tiếp
Cho các góc α , β và có số phức z = cos α + i.sin β . Khi đó x = z.w thì:
A . x = cos ( α - β ) + i . sin ( α + β )
B . x = cos ( α + β ) + i . sin ( α + β )
C . x = cos ( α β ) + i . sin ( α β )
D . x = sin ( α - β ) + i . cos ( α + β )
Cho
α
,
β
là các số thực. Đồ thị các hàm số
y
x
α
,
y
x
β
trên khoảng
0
;
+
∞
được cho hình vẽ bên. Khẳng định nào sau đây đúng? A.
0
β
1
α
B....
Đọc tiếp
Cho α , β là các số thực. Đồ thị các hàm số y = x α , y = x β trên khoảng 0 ; + ∞ được cho hình vẽ bên. Khẳng định nào sau đây đúng?
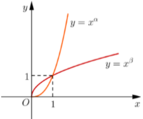
A. 0 < β < 1 < α
B. β < 0 < 1 < α
C. 0 < α < 1 < β
D. α < 0 < 1 < β
Cho α; β là các số thực. Đồ thị các hàm số y xα; y xβ trên khoảng (0; +∞) được cho hình vẽ bên. Khẳng định nào sau đây đúng? A.0 β1 α B.β 0 1 α . C.0α1β . D. α01β.
Đọc tiếp
Cho α; β là các số thực. Đồ thị các hàm số y= xα; y= xβ trên khoảng (0; +∞) được cho hình vẽ bên. Khẳng định nào sau đây đúng?
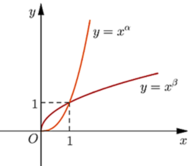
A.0< β<1< α
B.β< 0< 1< α .
C.0<α<1<β .
D. α<0<1<β.
Cho số phức z có phần thực và ảo đều khác 0. Gọi M và M’ là các điểm biểu diễn các số phức (-z) và
z
¯
. Chọn khẳng định đúng. A. M
≡
M B. M,M đối xứng nhau qua Oy C. M,M đối xứng nhau qua O D. M,M đối xứng nhau qua Ox
Đọc tiếp
Cho số phức z có phần thực và ảo đều khác 0. Gọi M và M’ là các điểm biểu diễn các số phức (-z) và z ¯ . Chọn khẳng định đúng.
A. M ≡ M'
B. M,M' đối xứng nhau qua Oy
C. M,M' đối xứng nhau qua O
D. M,M' đối xứng nhau qua Ox
Cho mặt phẳng
(
α
)
:
4
x
+
y
+
2
z
+
1
0
và
(
β
)
:
2
x
-
2
y
+
z
-
3
0
. Viết phương trình tham số của đường thẳng d là giao của
α
và
β
Đọc tiếp
Cho mặt phẳng ( α ) : 4 x + y + 2 z + 1 = 0 và ( β ) : 2 x - 2 y + z - 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của α và β
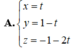
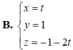
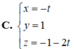
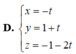
Trong mặt phẳng phức Oxy, tâp hợp các điểm biểu diễn số phức z sao cho z 2 là số thuần ảo là hai đường thẳng d1 ; d2. Góc α giữa 2 đường thẳng d1 ; d2 là bao nhiêu? A. α 450. B. α 600. C. α 900. D. α 300.
Đọc tiếp
Trong mặt phẳng phức Oxy, tâp hợp các điểm biểu diễn số phức z sao cho z 2 là số thuần ảo là hai đường thẳng d1 ; d2. Góc α giữa 2 đường thẳng d1 ; d2 là bao nhiêu?
A. α = 450.
B. α = 600.
C. α = 900.
D. α = 300.



