Góc ADB trên hình bs 3 có số đo bằng
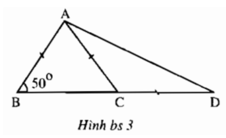
(A) 20o;
(B) 25o;
(C) 30o;
(D) 35o;
Hãy chọn phương án đúng.
Những câu hỏi liên quan
Cc ho tam giáABC có: ∠B - ∠C = 20o. Tia phân giác của góc A cắt BC tại D. tính số đo các góc ∠(ADC) , ∠(ADB)
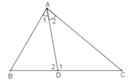
Trong ΔABD ta có ∠D1 là góc ngoài tại đỉnh D
∠D1 = ̂B + ∠A1 (tính chất góc ngoài của tam giác)
Trong ΔADC ta có ∠D2 là góc ngoài tại đỉnh D
∠D2 = ̂C + ∠A2 (tính chất góc ngoài của tam giác)
Ta có: ∠B > ∠C (gt); ∠A1 = ∠A2 (gt)
⇒∠D1 - ∠D2 = (B + ∠A1) - (C + ∠A2) = ∠B - ∠C = 20o
Lại có: ∠D1 + ∠D2 = 180o (hai góc kề bù)
⇒∠D1 = (180o + 20o):2 = 100o
⇒∠D1 = (100o - 20o) = 80o
Đúng 0
Bình luận (0)
Cho hình vẽ bên, biết Ax//By, góc A bằng 20o, góc B bằng 120o. Tính số đo x (góc C)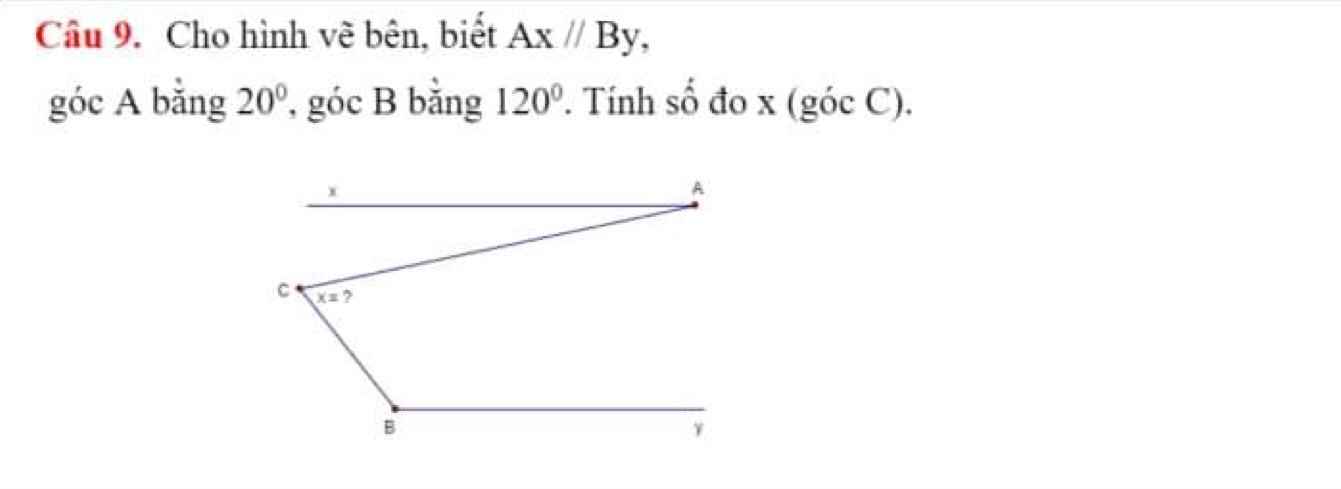
Trong hình vẽ sau, cho tam giác đều ABC và góc DBC bằng 20 độ.a. Kể tên các góc trong hình vẽ trên. Những góc nào có số đo bằng 60 độ?b. Điểm D có nằm trong góc ABC không? Điểm C có nằm trong góc ADB không?c. Em hãy dự đoán số đo góc ABD và sử dụng thước đo góc để kiểm tra lại dự đoán của mình.
Đọc tiếp
Trong hình vẽ sau, cho tam giác đều ABC và góc DBC bằng 20 độ.
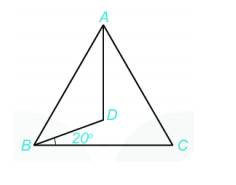
a. Kể tên các góc trong hình vẽ trên. Những góc nào có số đo bằng 60 độ?
b. Điểm D có nằm trong góc ABC không? Điểm C có nằm trong góc ADB không?
c. Em hãy dự đoán số đo góc ABD và sử dụng thước đo góc để kiểm tra lại dự đoán của mình.
a, Các góc có trong hình vẽ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB} ; \widehat{BDA} ; \widehat{DAB} ; \widehat{ABD} ; \widehat{DBC} ; \widehat{DAC}\)
Những góc có số đo bằng 60 độ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB}\)
b, Điểm D có nằm trong góc ABC. Điểm C không nằm trong góc ADB.
c, Số đo góc ABD là: 40o.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh bằng a. SA=SB=SC=SD=a. Số đo góc giữa hai vecto \(\overrightarrow{BD}\)và \(\overrightarrow{BS}\) bằng?
\(BD=a\sqrt{2}\)
\(\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=\widehat{SBD}=\dfrac{SB^2+BD^2-SD^2}{2SB.BD}=\dfrac{a^2+2a^2-a^2}{2a.a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=45^0\)
Đúng 1
Bình luận (3)
Tam giác ABC có
A
^
40
o
;
B
^
-
C
^
20
o
. Trên tia đối của tia AC lấy điểm E sao cho AEAB. Tính số đo góc CBE A. 80
°
B. 100
°
C. 90
°
D. 120
°
Đọc tiếp
Tam giác ABC có A ^ = 40 o ; B ^ - C ^ = 20 o . Trên tia đối của tia AC lấy điểm E sao cho AE=AB. Tính số đo góc CBE
A. 80 °
B. 100 °
C. 90 °
D. 120 °
+ Cho hình vẽ bên, biết góc ADB = 30°, góc KFC = 60°, AD = KC (học sinh không cần vẽ lại hình khi làm bài).a) Tính số đo của góc KCF.b) Hai tam giác trong hình có bằng nhau không? Giải thích?
Hình thang ABCD (AB//CD) có AB = 4cm; CD = 16cm và BD = 8cm, góc ADB bằng 40 độ . Tính số đo góc C của hình thang.
xét tam giác DBA và tam giác CDB có:
\(\dfrac{BA}{BD}=\dfrac{BD}{CD}\left(=\dfrac{1}{2}\right);\widehat{ABD}=\widehat{BDC}\) (so le trong)
=> △DBA ∼ △CDB (c-g-c)
=> \(\widehat{ADB}=\widehat{C}=40^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân à có góc a bằng 40 độ trên tia đối của tia CA lấy điểm D sao cho CD bằng CB . Tính số đo góc ADB
góc ACB=(180 độ -40 độ)/2=70 độ
suy ra góc BCD=180 độ -70 độ =110 độ
do CB=CD nên tam giác BCD cân tại C
suy ra góc CDB=(180 độ -110 độ)/2=35 độ
hay góc ADB =35 độ
Đúng 0
Bình luận (0)
Cho hình bs.4. Biết ∠ DOA = 120 ° , OA vuông góc với OC, OB vuông góc với OD. Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 180 ° ).
