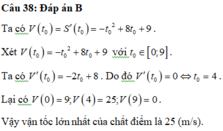Một chất điểm chuyển động theo quy luật s = 6 t 2 – t 3 . Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.

Những câu hỏi liên quan
Một chất điểm chuyển động theo quy luật s = 6 t 2 – t 3 . Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.
s = 6 t 2 − t 3 , t > 0
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3 t 2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+ ∞ ).
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = V C Đ = v(2) = 12(m/s).
Đúng 0
Bình luận (0)
Một chất điểm chuyển động theo quy luật s = 12 t 2 - 2 t 3 + 3 trong đó t là khoảng thời gian (tính bằng giây) mà chất điểm bắt đầu chuyển động. Tính thời điểm t (giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất.
A. t=2
B. t=4
C. t=1
D. t=3
Đáp án A
Ta có v = S ' = 24 t - 6 t 2 = - 6 ( t - 2 ) 2 + 24 ≤ 24 ( m / s ) ⇒ v m a x = 24 m / s đạt được khi t=2(giây)
Đúng 0
Bình luận (0)
Một chất điểm chuyển động theo quy luật \(s=6t^2-t^3\). Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất ?
Vận tóc của chuyển động là:
\(v=s'=12t-3t^2\)
Ta có \(v'=12-6t\)
\(v'=0\) khi t = 2 và \(v'\) đổi dấu từ dương sang âm khi đi qua t=2. Vậy \(v\) đạt giá trị lớn nhất khi t = 2.
Đúng 1
Bình luận (0)
Một chất chuyển động theo quy luật
s
6
t
2
-
t
3
(trong đó t là khoảng thừi gian tính bằng giây mà chất điểm bắt đầu chuyển động). Tính thời điểm t(giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất. A. t 1 B. t 3 C. t 2 D. t 4
Đọc tiếp
Một chất chuyển động theo quy luật s = 6 t 2 - t 3 (trong đó t là khoảng thừi gian tính bằng giây mà chất điểm bắt đầu chuyển động). Tính thời điểm t(giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất.
A. t = 1
B. t = 3
C. t = 2
D. t = 4
Một chất chuyển động theo quy luật
s
6
t
2
-
t
3
(trong đó t là khoảng thừi gian tính bằng giây mà chất điểm bắt đầu chuyển động). Tính thời điểm t(giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất. A. t 1 B. t 3 C. t 2 D. t 4
Đọc tiếp
Một chất chuyển động theo quy luật s = 6 t 2 - t 3 (trong đó t là khoảng thừi gian tính bằng giây mà chất điểm bắt đầu chuyển động). Tính thời điểm t(giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất.
A. t = 1
B. t = 3
C. t = 2
D. t = 4
Một chất điểm chuyển động theo quy luật
s
t
2
-
1
6
t
3
. Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất. A. t 0,5 B. t 1 C. t 2 D. t 2,5
Đọc tiếp
Một chất điểm chuyển động theo quy luật s = t 2 - 1 6 t 3 . Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.
A. t = 0,5
B. t = 1
C. t = 2
D. t = 2,5
Xét hàm số s = t 2 - 1 6 t 3 .
Vận tốc của chuyển động là v = y ' = 2 t - 1 2 t 2 .
Ta có v' = 2 - t; v' = 0 nên t = 2
Lập bảng biến thiên và suy ra m a x v t ∈ 0 ; + ∞ = 8 3 ⇔ t = 2
Đáp án C
Đúng 0
Bình luận (0)
Một chất điểm chuyển động theo quy luật S ( t ) = 6 t 2 – t 3 ; vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm t (s) bằng
A. 2 (s)
B. 12 (s)
C. 6 (s)
D. 4 (s)
Chọn A.
Vận tốc của chuyển động là v = s' tức là ![]()
![]()
Bảng biến thiên:
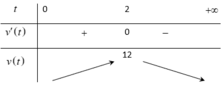
Hàm số v(t) đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+∞)
⇔ Max v(t) = 12 khi t = 2.
Vận tốc đạt giá trị lớn nhất bằng 12 khi t = 2(s).
Đúng 0
Bình luận (0)
Một chất điểm chuyển động theo quy luật
S
6
t
2
−
t
3
vận tốc
v
m
/
s
của chuyển động đạt giá trị lớn nhất tại thời điểm t(s) bằng A. 2 s B. 6s C. 12s D. 4s
Đọc tiếp
Một chất điểm chuyển động theo quy luật S = 6 t 2 − t 3 vận tốc v m / s của chuyển động đạt giá trị lớn nhất tại thời điểm t(s) bằng
A. 2 s
B. 6s
C. 12s
D. 4s
Đáp án A
Phương trình vận tốc của vật: v = S ' t = 12 t − 3 t 2 = − 3 t − 2 2 + 12 ≤ 12
Do đó vận tốc đạt giá trị lớn nhất khi t = 2 s
Đúng 0
Bình luận (0)
Một chất điểm chuyển động theo quy luật
S
-
1
3
t
3
+
4
t
2
+
9
t
với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và S (mét) là quãng đường vật chuyển động trong thời gian đó.Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của chất điểm là bao nhiêu? A.
88
(
m...
Đọc tiếp
Một chất điểm chuyển động theo quy luật S = - 1 3 t 3 + 4 t 2 + 9 t với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và S (mét) là quãng đường vật chuyển động trong thời gian đó.Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của chất điểm là bao nhiêu?
A. 88 ( m / s )
B. 25 ( m / s )
C. 100 ( m / s )
D. 11 ( m / s )