Dựa vào đồ thị vận tốc – thời gian của chất điểm được mô tả như hình bên. Gọi a 1 ; a 2 và a 3 lần lượt là gia tốc chuyển động của chất điểm trên đoạn OA; AB và BC. Giá trị a 1 + a 2 + a 3 bằng
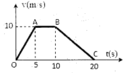
A. 1m/s2.
B. 2m/s2.
C. 0m/s2.
D. -1m/s2.
Cho một chất điểm đang dao động điều hòa. Đồ thị phụ thuộc của li độ (x) vào thời gian (t) được mô tả như hình vẽ. Biểu thức của vận tốc tức thời của chất điểm có dạng
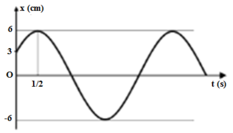
A. v = 4πcos(2πt/3 + 5π/6) cm/s
B. v = 4πcos(2πt/3 + π/6) cm/s
C. v = 4π2cos(2πt/3 + 5π/6) cm/s
D. v = 4πcos(πt/3 + π/6) cm/s
Cho một chất điểm đang dao động điều hòa. Đồ thị phụ thuộc của li độ (x) vào thời gian (t) được mô tả như hình vẽ. Biểu thức của vận tốc tức thời của chất điểm có dạng
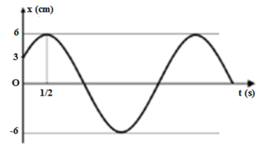
A. v = 4πcos(2πt/3 + 5π/6) cm/s
B. v = 4πcos(2πt/3 + π/6) cm/s
C. v = 4π2cos(2πt/3 + 5π/6) cm/s
D. v = 4πcos(πt/3 + π/6) cm/s
Đáp án B
Ta có T/6 = 1/2 s → T = 3 s → ω = 2π/3 rad/s.
Tại t = 0: x = A/2 theo chiều dương → φ = π/3.
Phương trình li độ x = 6cos(2πt/3 – π/3) cm.
→ v = 4πcos(2πt/3 + π/6) (cm/s)
Cho một chất điểm đang dao động điều hòa. Đồ thị phụ thuộc của li độ (x) vào thời gian (t) được mô tả như trên hình vẽ. Biểu thức gia tốc tức thời của chất điểm là
A. a = 8 πcos πt - π 3 cm / s 2
B. a = 8 πcos πt + π 3 cm / s 2
C. a = 8 π 2 cos πt + 2 π 3 cm / s 2
D. a = 8 π 2 cos πt - 2 π 3 cm / s 2
Chất điểm chuyển động có đồ thị vận tốc theo thời gian như hình 7P1
a) Mô tả chuyển động của chất điểm.
b) Tính quãng đường mà chất điểm đi được từ khi bắt đầu chuyển động cho tới khi dừng lại.
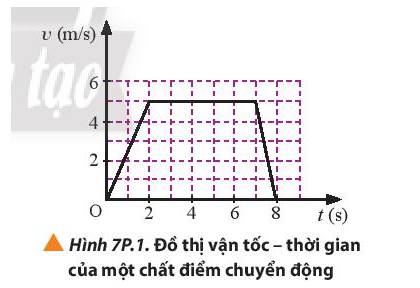
a) Mô tả chuyển động của chất điểm:
+ Từ 0 – 2 s, vật chuyển động thẳng nhanh dần đều
+ Từ 2 – 7 s, vật chuyển động thẳng đều
+ Từ 7 – 8 s, vật chuyển động thẳng chậm dần đều
b) Quãng đường vật đi được trong 2 s đầu là:
\({a_1} = \frac{{5 - 0}}{2} = 2,5(m/{s^2}) \Rightarrow {s_1} = \frac{{{5^2} - {0^2}}}{{2.2}} = 6,25(m)\)
Quãng đường vật đi được từ 2 – 7 s là:
\({s_2} = 5.(7 - 2) = 25(m)\)
Quãng đường vật đi được từ 7 – 8 s là:
\({a_3} = \frac{{0 - 5}}{{8 - 7}} = - 5(m/{s^2}) \Rightarrow {s_3} = \frac{{{0^2} - {5^2}}}{{2.( - 5)}} = 2,5(m)\)
=> Quãng đường mà chất điểm đi được từ lúc bắt đầu đến khi dừng hẳn là:
S = 6,25 + 25 + 2,5 = 33,75 (m)
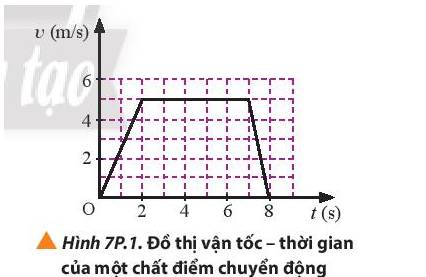
4. Chất điểm chuyển động có đồ thị vận tốc theo thời gian như hình 7P1
a) Mô tả chuyển động của chất điểm.
b) Tính quãng đường mà chất điểm đi được từ khi bắt đầu chuyển động cho tới khi dừng lại.
Dựa vào các đồ thị trong Hình 2.3:
a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.
b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,5 s; 0,75 s và 1 s
c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b
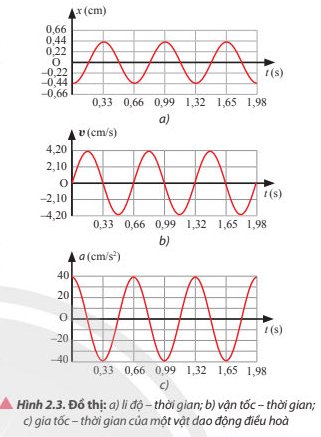
Biên độ dao động: A = 0,44 cm
Tốc độ cực đại: vmax = 4,2 cm/s
Gia tốc cực đại: amax = 40 cm/s2
Chu kì của gia tốc của vật: T = 0,66 s.
Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)
a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ0 = π(rad)
Khi đó, phương trình li độ có dạng:
x = Acos(ωt+φ0) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)
Phương trình vận tốc có dạng:
v = ωAcos(ωt+φ0+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)
Phương trình gia tốc có dạng:
a = −ω2Acos(ωt+φ0) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s2)
b)
Từ đồ thị có thể thấy:
t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s2
t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s2
t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s2
c) Nghiệm lại với các phương trình.
- Tại thời điểm t = 0,5 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)
v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)
a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s2)
- Tại thời điểm t = 0,75 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s2)
- Tại thời điểm t = 1 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s2)
Một chất điểm dao động điều hòa có đồ thị biểu diễn sự phụ thuộc của gia tốc a vào thời gian t như hình vẽ bên. Ở thời điểm t = 0, vận tốc của chất điểm là
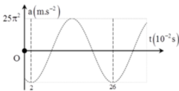
A. 0,75π m/s.
B. 3π m/s.
C. 1,5π m/s.
D. –1,5π m/s.
Một chất điểm dao động điều hòa có đồ thị biểu diễn sự phụ thuộc của gia tốc a vào thời gian t như hình vẽ bên. Ở thời điểm t = 0, vận tốc của chất điểm là
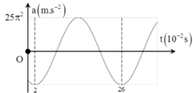
A. 0,75π m/s.
B. 3π m/s.
C. 1,5π m/s.
D. –1,5π m/s
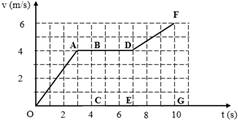
Câu 1: Một chất điểm chuyển động có đồ thị vận tốc theo thời gian như hình sau
a. Mô tả chuyển động của chất điểm.
b. Tính quãng đường mà chất điểm đi được từ khi bắt đầu chuyển động cho tới giây thứ 10.
c. Tính độ dịch chuyển của chất điểm từ khi bắt đầu chuyển động đến thời điểm 5s. Tính vận tốc trung bình trong thời gian đó.
d. Tính vận tốc trung bình và tốc độ trung bình khi bắt đầu chuyển động đến thời điểm 7s