Phương trình 2 sin 2 x - 5 sin x cos x - cos 2 x = -2 tương đương với:
A. 3cos2x + 5sin2x = 5
B. 3cos2x + 5sin2x = -5
C. 3cos2x - 5sin2x= 5
D. 3cos2x - 5sin2x = -5
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2)
B. (1)
C. (3)
D. (1) và (2)
Trong các phương trình sau: cos x = 5 - 3 (1); sin x = 1 - 2 (2); sin x + cos x = 2 (3), phương trình nào vô nghiệm?
A. (2).
B. (1).
C. (3).
D. (1) và (2).
Chọn C
Ta có: ![]() nên (1) và (2) có nghiệm.
nên (1) và (2) có nghiệm.
Cách 1:
Xét: ![]()
![]() nên (3) vô nghiệm.
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 

nên (3) vô nghiệm.
giải phương trình sin^2 x − 4√3 sin x · cos x + cos^2 x = −2.
Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Giải các phương trình sau :
a) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
b) \(3\sin^2-4\sin x\cos x+5\cos^2x=2\)
c) \(\sin^2x+\sin2x-2\cos^2+5\cos^2x=2\)
d) \(2\cos^2x-3\sqrt{3}\sin2x-4\sin^2x=-4\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 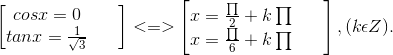
Giải các phương trình sau :
a) \(\cos^2x+2\sin x\cos x+5\sin^2x=2\)
b) \(3\cos^2x-2\sin2x+\sin^2x=1\)
c) \(4\cos^2x-3\sin x\cos x+3\sin^2x=1\)
Giải các phương trình sau:
\(5\sin^22x-6\sin4x-2\cos^2x=0\)
\(2\sin^23x-10\sin6x-\cos^23x=-2\)
\(\sin^2x\left(\tan x+1\right)=3\sin x\left(\cos x-\sin x\right)+3\)
\(6\sin x-2\cos^3x=\frac{5\sin4x.\cos x}{2\cos2x}\)
Đưa về tích rồi giải các phương trình sau:
a) \(\sin 2x -2.\sin x +\cos x -1=0\)
b) \(\sqrt{2} . (\sin x - 2.\cos x) = 2-\sin 2x\)
c) \(\frac{1}{\cos x} - \frac{1}{\sin x}=2\sqrt 2 .\cos(x + \frac{\pi}{4}) \)
\(a,sin2x-2sinx+cosx-1=0\)
\(\Leftrightarrow2sinxcosx-2sinx+cosx-1=0\)
\(\Leftrightarrow2sinx\left(cosx-1\right)+cosx-1=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=1\\sinx=-\frac{1}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2k\pi\\x=\frac{-\pi}{6}+2k\pi\end{cases}}}\)
\(b,\sqrt{2}\left(sinx-2cosx\right)=2-sin2x\)
\(\Leftrightarrow\sqrt{2}sinx-2\sqrt{2}cosx-2+2sinxcosx=0\)
\(\Leftrightarrow\sqrt{2}sinx\left(1+\sqrt{2}cosx\right)-2.\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{2}cosx+1\right)\left(\sqrt{2}sinx-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=\frac{-\sqrt{2}}{2}\\sinx=\frac{2\sqrt{2}}{2}\left(l\right)\end{cases}}\)(vì \(-1\le sinx\le1\))
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3\pi}{4}+2k\pi\\x=\frac{5\pi}{4}+2k\pi\end{cases}}\)
\(c,\frac{1}{cosx}-\frac{1}{sinx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\frac{sinx-cosx}{sinx.cosx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\frac{-\sqrt{2}cos\left(x+\frac{\pi}{4}\right)}{sinx.cosx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow sin2x+1=0\)
\(\Leftrightarrow sin2x=-1\)
\(\Leftrightarrow2x=\frac{3\pi}{2}+2k\pi\)
\(\Leftrightarrow x=\frac{3\pi}{4}+k\pi\)
@Bùi Nhật Vy, Bạn nhớ kĩ cái này nha
\(asinx+bcosx=\sqrt{a^2+b^2}sin\left(x+\alpha\right)=-\sqrt{a^2+b^2}cos\left(x-\alpha\right)\)
trong đó \(\cos\alpha=\frac{a}{\sqrt{a^2+b^2}},sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\)
Giải phương trình
\(\sin\dfrac{5x}{2}=5\cos^3x\sin\dfrac{x}{2}\)
Giải phương trình lượng giác sau
1) 2 cos 2x -\(\sqrt{3}\) = 0
2)\(\sqrt{3}\) tan x + 1 = 0
3) 2 cos2x = 1
4) 6 sin2 x- 13 sin x + 5 = 0
5) 5 cos 2x + 6 cos x + 1 = 0
6 ) 2 cos 2 2x - 3 cos 2x + 1 = 0
7) tan 2 x + ( 1 - \(\sqrt{3}\)) tan x - \(\sqrt{3}\) = 0
8) cos 6x + 2 sin 3x + 3 = 0
9) cos 2x - 4 cos x - 5 = 0
10 ) 3 cos 2 x = 2 sin 2 x + 4 sin x
11) cos 2x + sin2x + 2 cos x + 1 = 0
12) cos 4x + sin 4x + sin 2x = \(\dfrac{5}{2}\)