Hàm số y = tan 3 x / sin 3 x thỏa mãn tính chất nào sau đây?
A. Hàm chẵn.
B. Hàm không có tính chẵn, lẻ.
C. Xác định trên R.
D. Hàm lẻ.
Những câu hỏi liên quan
Trong các hàm số
y
tan
x
;
y
sin
2
x
;
y
sin
x
;
y
c
o
t
x
có bao nhiêu hàm số thỏa mãn tính chất
f
x
+
k
π
f...
Đọc tiếp
Trong các hàm số y = tan x ; y = sin 2 x ; y = sin x ; y = c o t x có bao nhiêu hàm số thỏa mãn tính chất f x + k π = f x ; ∀ x ∈ ℝ ; k ∈ ℤ
A. 3
B. 2
C. 1
D. 4
Đáp án C
Hàm số y = sin 2x thỏa mãn tính chất trên, các hàm số y = tan x, y = cot x cần điều kiện của x.
Đúng 0
Bình luận (0)
1. Mệnh đề nào dưới đây sai ?A. Hàm số y tan x là hàm số lẻ. B. Hàm số y sin x là hàm số lẻC. Hàm số y Cot x là hàm số lẻ D. Hàm số y Cos x là hàm số lẻ2. Hàm số nào sau đây là hàm số lẻ?A. y Cos3x B. y Sinx + Cos3xC. y Sinx + Tan3x D. Tan2x3. Trong các hàm số sau, hàm số nào là hàm số chẵnA. y Cos2x B. y Cot2xC. y tan2x D. y sin2x4. Trong các hàm số sau, hàm số nào là hàm số lẻ?A. y Sinx Co...
Đọc tiếp
1. Mệnh đề nào dưới đây sai ?
A. Hàm số y = tan x là hàm số lẻ. B. Hàm số y = sin x là hàm số lẻ
C. Hàm số y = Cot x là hàm số lẻ D. Hàm số y = Cos x là hàm số lẻ
2. Hàm số nào sau đây là hàm số lẻ?
A. y = Cos3x B. y = Sinx + Cos3x
C. y = Sinx + Tan3x D. Tan2x
3. Trong các hàm số sau, hàm số nào là hàm số chẵn
A. y = Cos2x B. y = Cot2x
C. y = tan2x D. y = sin2x
4. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. y = Sinx Cos3x
B. y = Cosx + Sin2x
C. y = Cosx + Sinx
D. y = - Cosx
5. Hàm số nào là hàm số chẵn ?
A. y = Cosx
B. y = Sin x/2
C. y = tan2x
D. y = Cotx
Cho hàm số y sin x.a) Xét tính chẵn, lẻ của hàm sốb) Hoàn thành bảng giá trị sau của hàm số y sin x trên đoạn left[ { - pi ;pi } right] bằng cách tính giá trị của sin x với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của sin x với những x âm. x - pi - frac{{3pi }}{4} - frac{pi }{2} - frac{pi }{4}0 frac{pi }{4} frac{pi }{2} frac{{3pi }}{4} pi sin x?????????Bằng cách lấ...
Đọc tiếp
Cho hàm số \(y = \sin x\).
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị sau của hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) bằng cách tính giá trị của \(\sin x\) với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của \(\sin x\) với những x âm.
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm \(M\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = 2\pi \), ta được đồ thị của hàm số \(y = \sin x\) như hình dưới đây.
Từ đồ thị ở Hình 1.14, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số \(y = \sin x\)
a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) = - \sin x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \sin x\) là hàm số lẻ.
b)
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | \(0\) | \( - \frac{{\sqrt 2 }}{2}\) | \( - 1\) | \( - \frac{{\sqrt 2 }}{2}\) | 0 | \(\frac{{\sqrt 2 }}{2}\) | 1 | \(\frac{{\sqrt 2 }}{2}\) | 0 |
c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)
Đúng 0
Bình luận (0)
Quan sát đồ thị hàm số y sin x ở Hình 25.a) Nêu tập giá trị của hàm số y sin xb) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y sin xc) Bằng cách dịch chuyển đồ thị hàm số y sin x trên đoạn left[ { - pi ;pi } right] song song với trục hoành sang phải theo đoạn có độ dài 2pi , ta có nhận được đồ thị hàm số y sin x trên đoạn left[ {pi ;3pi } right] hay không? Hàm số y sin xcó tuần hoàn hay không/d) Tìm khoảng đồng biến, nghịch...
Đọc tiếp
Quan sát đồ thị hàm số \(y = \sin x\) ở Hình 25.
a) Nêu tập giá trị của hàm số \(y = \sin x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \sin x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta có nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \sin x\)có tuần hoàn hay không/
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \sin x\)
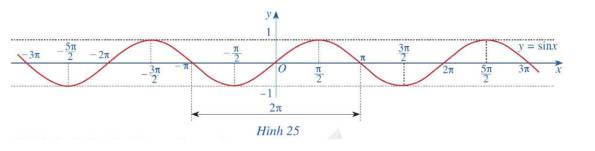
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)
Đúng 0
Bình luận (0)
Trong các hàm số sau đây, hàm số nào là hàm tuần hoàn?
A. \(y = \tan x + x\)
B. \(y = {x^2} + 1\)
C. \(y = \cot x\)
D. \(y = \frac{{\sin x}}{x}\)
Hàm \(y = \cot x\)là hàm tuần hoàn với chu kì \(T = \pi \)do :
- Tập xác định là \(D = R\backslash \left\{ {k\pi ;k \in Z} \right\}\)
- Với mọi \(x \in D\), ta có \(x - \pi \; \in D\) và \(x + \pi \in D\;\)
Suy ra
\(\begin{array}{l}f\left( {x + \pi } \right) = \cot \left( {x + \pi } \right) = \cot \left( x \right) = f(x)\\f\left( {x - \pi } \right) = \cot \left( {x - \pi } \right) = \cot \left( x \right) = f\left( x \right)\end{array}\)
Đúng 0
Bình luận (0)
Trong các hàm số sau đây: y = -|x|x2; y = x2 + 4|x|; y = -x4 + 2x2 có bao nhiêu hàm số chẵn?
A. Không có B. Một hàm số chẵn C. Hai hàm số chẵn D. Ba hàm số chẵn
Trong các hàm số sau đây: y = |x|x2; y = x4 + 4|x|; y = -7x4 + 2x2 có bao nhiêu hàm số chẵn?
A. Không có B. Một hàm số chẵn C. Hai hàm số chẵn D. Ba hàm số chẵn.
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 10:44
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Đúng 1
Bình luận (0)
Cho y
x
cos
2
x
trên
-
π
2
;
π
2
và F(x) là một nguyên hàm của hàm số xf ‘(x) thỏa mãn F(0) 0. Biết
a
∈
-...
Đọc tiếp
Cho y = x cos 2 x trên - π 2 ; π 2 và F(x) là một nguyên hàm của hàm số xf ‘(x) thỏa mãn F(0) = 0. Biết a ∈ - π 2 ; π 2 thỏa mãn tan a = 3. Tính F(a) – 10a2 + 3a
A. 1 2 ln 10
B. - 1 4 ln 10
C. - 1 2 ln 10
D. ln 10
Đáp án A
Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)
Cách giải:
=> 
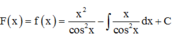
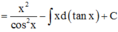
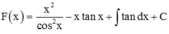
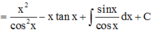
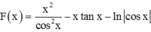
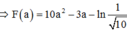
Đúng 0
Bình luận (0)