\(a,y'=\left(x^3-4x^2+5\right)'=3x^2-8x\\ b,y''=\left(3x^2-8x\right)'=6x-8\)

1) \(f\left(x\right)=2x-5\)

\(f'\left(x\right)=2\)

\(\Rightarrow f'\left(4\right)=2\)

2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)

\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)

3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)

\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)

\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)

1. \(y'=3x^2\sqrt{x}+\dfrac{x^3-5}{2\sqrt{x}}=\dfrac{7x^3-5}{2\sqrt{x}}\)

2. \(y'=3x^5+\dfrac{3}{x^2}+\dfrac{1}{\sqrt{x}}\)

3. \(y'=2-\dfrac{2}{\left(x-2\right)^2}\)

a.

\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)

b.

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)

Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)

\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)

\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)

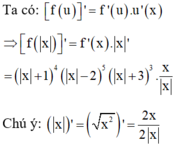
Do đó hàm số f(|x|)  có 3 điểm cực trị  tại x= 2; x= -2 và  x= 0

Chọn B.

a) \(g'\left( x \right) = y' = {\left( {2x + \frac{\pi }{4}} \right)^,}.\cos \left( {2x + \frac{\pi }{4}} \right) = 2\cos \left( {2x + \frac{\pi }{4}} \right)\)

b) \(g'\left( x \right) =  - 2{\left( {2x + \frac{\pi }{4}} \right)^,}.\sin \left( {2x + \frac{\pi }{4}} \right) =  - 4\sin \left( {2x + \frac{\pi }{4}} \right)\)

Chọn A

Áp dụng công thức

Hàm \(y=\dfrac{ax+b}{cx+d}\) có đạo hàm \(y'=\dfrac{ad-bc}{\left(cd+d\right)^2}\)

Do đó: \(y'=\dfrac{5m-n}{\left(x+5\right)^2}\)

Chọn C

a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:

\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)

Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).

b) Ta có:

\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)