Tính tích phân I = ∫ 0 π 2 x cos x ( a - x ) d x .
A. I = 1 - π 2 cos a + sin a
B. I = π 2 - 1 cos a - sin a
C. I = π 2 - 1 cos a + sin a
D. I = π 2 + 1 cos a - sin a
Những câu hỏi liên quan
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho hàm số yf(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx1, x ϵ [0;π/3] và f(0)1. Tính tích phân
I
∫
0
π
3
f
x
d
x
A. 1/2 + π/3 B.
3
+
1
2
C. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng
y
cos
x
,
y
0
,
x
0
,
x
π
quay quanh trục Ox. A.
π
3
B.
π
2
2
C.
π
2
D. ...
Đọc tiếp
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng y = cos x , y = 0 , x = 0 , x = π quay quanh trục Ox.
A. π 3
B. π 2 2
C. π 2
D. π 2 3
Tìm tất cả giá trị của m để phương trình:
cos 2x + (2m - 3) sin x + m - 2 = 0 có đúng 2 nghiệm phân biệt x thuộc [-π/2 ; π/2]
Xem chi tiết
\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tính thể tích khối tròn xoay đó hình phẳng giới hạn bởi các đường sau quay quanh Ox:
y = cos x;y = 0; x = π
Dựa vào đồ thị y = cos x trên [-π,π] hãy chỉ ra các khoảng giá trị x mà cos x >0 , cos x < 0
Cho hai số thực a và b thỏa mãn a b và
∫
a
b
x
sin
x
d
x
π
đồng thời a cos a 0 và
b
cos
b
-
π
.Tính tích phân
∫
a
b
cos
x
d
x
. A.
I
-
π
.
B.
I...
Đọc tiếp
Cho hai số thực a và b thỏa mãn a < b và ∫ a b x sin x d x = π đồng thời a cos a = 0 và b cos b = - π .Tính tích phân ∫ a b cos x d x .
A. I = - π .
B. I = π .
C. I = 145 12 .
D. I = 0.
Chọn D.
Đặt u = x d v = sin x d x ⇒ d u = d x v = - cos x
Đúng 0
Bình luận (0)
Diện tích hình phẳng giới hạn bởi các đường cong y sin x; y cos x và các đường thẳng
x
0
,
x
π
bằng A.
3
2
B.
2
C.
2
2
D. -
2
2
Đọc tiếp
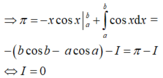
Diện tích hình phẳng giới hạn bởi các đường cong y = sin x; y= cos x và các đường thẳng x = 0 , x = π bằng
A. 3 2
B. 2
C. 2 2
D. - 2 2
Đáp án C
Giải phương trình: s inx = cos x ⇒ x = π 4 (vì 0 ≤ x ≤ π )
S = ∫ 0 π s inx − cos x d x = 2 2
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
Đúng 0
Bình luận (0)