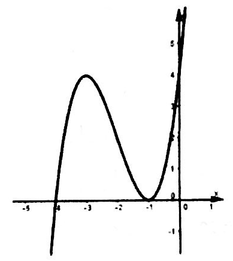
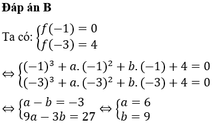Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B. I 0 ; - 3 2
C. I 0 ; 3 2
D. I(-2;2)