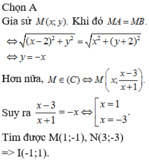Các câu hỏi tương tự
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
. Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN A.
M
N
4
2
B. MN 3 C.
M
N
2
2...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN
A. M N = 4 2
B. MN = 3
C. M N = 2 2
D. M N = 3 5
Gọi M và N là giao điểm của đồ thị hai hàm số y = x 4 − 2 x 2 + 2 v à y = − x 2 + 4 . Tọa độ trung điểm I của đoạn thẳng MN là
A. (1;0)
B. (0;2)
C. (2;0)
D. (0;1)
Gọi (C) là đồ thị hàm số
y
x
-
7
x
+
1
, A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho
0
x
M
3
, tìm giá trị lớn nhất của diện tích
∆
A
B
M
A. 3 B. 5 C. 6 D....
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0 < x M < 3 , tìm giá trị lớn nhất của diện tích ∆ A B M
A. 3
B. 5
C. 6
D. 3 5
Gọi (C) là đồ thị hàm số
y
x
-
7
x
+
1
, A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0xM3, tìm giá trị lớn nhất của diện tích
∆
A
M
B
A. 3 B. 5 C. 5 D. 3
5
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x - 7 x + 1 , A, B là các điểm thuộc (C) có hoành độ lần lượt là 0 và 3. M là điểm thay đổi trên (C) sao cho 0<xM<3, tìm giá trị lớn nhất của diện tích ∆ A M B
A. 3
B. 5
C. 5
D. 3 5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ). Diện tích hình phẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x 0; x 2 có diện tích bằng
28
5
(phần gạch chéo tro...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm
A
−
1
;
0
. Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0, x2 bằng...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hai hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
với
a
≠
0
và g(x)
p
x
2
+
q
x
-
3
c
ó
đồ thị như...
Đọc tiếp
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho hàm số
y
2
x
-
1
2
x
-
2
có đồ thị (C). Gọi
M
x
0
;
y
0
(với
x
0
1
) là điểm thu...
Đọc tiếp
Cho hàm số y = 2 x - 1 2 x - 2 có đồ thị (C). Gọi M x 0 ; y 0 (với x 0 > 1 ) là điểm thuộc (C), biết tiếp tuyến của (C) tại M cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S ∆ O I B = 8 S ∆ O I A (trong đó O là gốc tọa độ, I là giao điểm hai tiệm cận). Giá trị của S = x 0 + 4 y 0 bằng
A. 8
B. 2
C. 17 4
D. 23 4