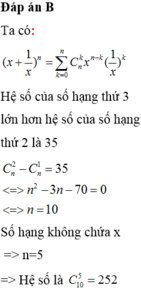Tìm số hạng không chứa x trong khai triển của x 3 + 1 x 8

Những câu hỏi liên quan
a)Tìm số hạng không chứa x trong khai triển (x+2/x)10
b)Tìm số hạng không chứa x trong khai triển (x+2/x2)6
c)Tìm hệ số của số hạng chứa x10 trong khai triển (3x3-2/x2)5
a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810
Đúng 1
Bình luận (0)
Trong khai triển nhị thức
x
+
1
x
n
,
x
≠
0
, hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên. A. 225 B. 252 C. 522 D. 525
Đọc tiếp
Trong khai triển nhị thức x + 1 x n , x ≠ 0 , hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Trong khai triển nhị thức
x
+
1
x
n
,
x
≠
0
hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên. A. 225 B. 252 C. 522 D. 525
Đọc tiếp
Trong khai triển nhị thức x + 1 x n , x ≠ 0 hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
1. Tìm hệ số của số hạng x^4 trong khai triển left(x-3right)^92. Tìm hệ số của số hạng chứa x^{12}y^{13} trong khai triển left(2x+3yright)^{25}3. Tìm hệ số của số hạng chứa x^4 trong khai triển left(dfrac{x}{3}-dfrac{3}{x}right)^{12}4. Tìm hệ số của số hạng không chứa x trong khai triển left(x^2-dfrac{1}{x}right)^65. Tìm hệ số của số hạng không chứa x trong khai triển left(x+dfrac{1}{x^4}right)^{10}
Đọc tiếp
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Tìm số hạng không chứa x trong khai triển của
x
2
-
1
x
12
. A. -459. B. -495. C. 495. D. 495.
Đọc tiếp
Tìm số hạng không chứa x trong khai triển của x 2 - 1 x 12 .
A. -459.
B. -495.
C. 495.
D. 495.
Đáp án C
Phương pháp:
Sử dụng công thức khai triển nhị thức Newton:
![]()
Cách giải
Ta có :
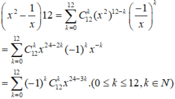
Để có số hạng không chứa x trong khai triển thì:
![]()
Vậy hệ số cần tìm là
![]()
Đúng 0
Bình luận (0)
Tìm số hạng không chứa x trong khai triển nhị thức Newton của (1/x +x³)⁴
SHTQ là: \(C^k_4\cdot\left(x^3\right)^{4-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_4\cdot x^{12-4k}\)
Số hạng ko chứa x tương ứng với 12-4k=0
=>k=3
=>SH đó là \(C^3_4=4\)
Đúng 2
Bình luận (0)
Tìm hệ số của số hạng không chứa x trong khai triển
x
2
+
4
x
18
với
x
≠
0
Đọc tiếp
Tìm hệ số của số hạng không chứa x trong khai triển x 2 + 4 x 18 với x ≠ 0
![]()
![]()
![]()
![]()
Tìm hệ số của số hạng không chứa x trong khai triển
x
2
+
4
x
18
v
ớ
i
x
≠
0
.
A
.
2
11
....
Đọc tiếp
Tìm hệ số của số hạng không chứa x trong khai triển x 2 + 4 x 18 v ớ i x ≠ 0 .
A . 2 11 . C 18 7
B . 2 8 . C 18 8
C . 2 9 . C 18 9
D . 2 8 . C 18 10
Chọn C
Ta có: 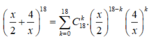
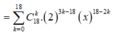
![]()
Số hạng tổng quát trong khai triển ![]()
![]()
Số hạng không chứa x trong khai triển phải có: ![]()
=> 18 - 2k = 0 => k = 9
Suy ra hệ số của số hạng không chứa x trong khai triển là: ![]()
Đúng 0
Bình luận (0)