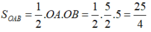Ta có: \(y'\left(\dfrac{1}{2}\right)=2\cdot\dfrac{1}{2}=1\)

Vậy hệ số góc của tiếp tuyến của parabol \(y=x^2\) tại điểm có hoàng độ \(x_0=\dfrac{1}{2}\) là k = 1.

Ta có:

 \(y'=\left(-2x^2\right)'=-4x\Rightarrow y'\left(-1\right)=-4\cdot\left(-1\right)=4\)

\(y_0=-2\cdot\left(-1\right)^2=-2\)

Phương trình tiếp tuyến là: \(y=4\left(x+1\right)-2=4x+2\)

Đáp án A

Ta có: y ' = − 6 x + 1 ⇒ y ' 1 = − 5.  

Do đó phương trình tiếp tuyến của parabol tại M là y = − 5 x − 1 = − 5 x + 5.

Gọi phương trình tiếp tuyến d tại A của parabol có dạng \(y=4x+b\) (\(b\ne5\))

Pt hoành độ giao điểm d và (P):

\(x^2=4x+b\Leftrightarrow x^2-4x-b=0\) (1)

d tiếp xúc (P) \(\Leftrightarrow\) (1) có nghiệm kép

\(\Leftrightarrow\Delta'=4+b=0\Rightarrow b=-4\)

Hoành độ giao điểm: \(x=\frac{4}{2.1}=2\Rightarrow y=4\Rightarrow A\left(2;4\right)\)

Với \({x_0}\) bất kì, ta có:

\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - {x^2} + 4x + x_0^2 - 4{x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - \left( {{x^2} - x_0^2} \right) + 4\left( {x - {x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( { - x - {x_0} + 4} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( { - x - {x_0} + 4} \right) =  - 2{x_0} + 4\)

Vậy hàm số \(y =  - {x^2} + 4x\) có đạo hàm là hàm số \(y' =  - 2x + 4\)

a) Ta có \(y'\left( 1 \right) =  - 2.1 + 4 = 2\)

Ngoài ra , \(f\left( 1 \right) = 3\) nên phương trình tiếp tuyến cần tìm là:

\(y - 3 = 2\left( {x - 1} \right)\) hay \(y = 2x + 1\)

b) Ta có \({y_0} = 0\) nên \( - x_0^2 + 4{x_0} = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 0\\{x_0} = 4\end{array} \right.\)

+) \({x_0} = 0,{y_0} = 0\) nên \(y'\left( 0 \right) = 4\) do đó phương trình tiếp tuyến cần tìm là \(y = 4x\)

+) \({x_0} = 4,{y_0} = 0\) nên \(y'\left( 4 \right) =  - 4\) do đó phương trình tiếp tuyến cần tìm là

\(y =  - 4\left( {x - 4} \right)\) hay \(y =  - 4x + 16\)

Ta có \(y=x^4-4x^3+4x^2\Rightarrow4x^3-12x^2+8x\)

a. PTHD giao điểm của (C) và Parabol \(y=x^2\) :

\(x^4-4x^3+4x^2=x^2\Leftrightarrow x^2\left(x^2-4x+3\right)=0\)

                                \(\Leftrightarrow x=0;x=1;x=3\)

* \(x=0\) ta có phương trình tiếp tuyến là \(y=0\)

* \(x=2\) ta có phương trình tiếp tuyến là \(y=1\)

* \(x=3\) ta có phương trình tiếp tuyến là \(y=24x-63\)

b. Gọi d là đường thẳng đi qua A, có hệ số góc k \(\Rightarrow d:y=k\left(x-2\right)\)

d là tiếp tuyến \(\Leftrightarrow\begin{cases}\left(2-x\right)^2x^2-k\left(x-2\right)\\4x\left(x-2\right)\left(x-1\right)=k\end{cases}\) có nghiệm

Thay k vào phương trình thứ nhất ta có :

\(x^4-4x^3+4x^2=\left(x-2\right)\left(4x^3-12x^2+8x\right)\)

\(\Leftrightarrow x\left(3x-4\right)\left(x-2\right)^2=0\)

\(\Leftrightarrow x=0;x=2;x=\frac{4}{3}\)

* \(x=0\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)

* \(x=2\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)

Chọn B

Ta có y’=-2x; y’(1)=-2. Phương trình tiếp tuyến của y = 4 - x 2  tại điểm (1,3) là

(d):y= -2(x-1)+3=-2x+5.

Đường thẳng (d) cắt trục hoành tại điểm A(5/2; 0) và cắt trục tung tại B(0;5).

Ta có: OA = 5/2; OB = 5

Diện tích tam giác OAB vuông tại O là