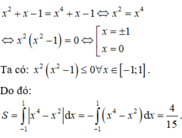Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
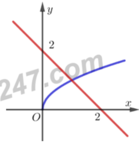
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = 2 , x = 0 và x = 1.
A. S = 4 ln 2 + e - 5
B. S = 4 ln 2 + e - 6
C. S = e 2 - 7
D. S = e - 3
Đáp án A
Phương trình hoành độ giao điểm e x = 2 ⇔ x = ln 2
Suy ra diện tích cần tìm bằng S = ∫ 0 ln 2 e x - 2 d x + ∫ ln 2 0 e x - 2 d x = 4 ln 2 + e - 5 .
Tính diện tích hình phẳng giới hạn bởi các đường:
y = x 2 + 1; x = -1; x = 2 và các trục hoành.
Tính diện tích các hình phẳng giới hạn bởi các đường sau: y = x - 1 + lnx x , y = x - 1 và x = e
Diện tích hình phẳng giới hạn bởi các đường y = e x ; y = 1 v à x = 1 là
A. e - 2.
B. e.
C. e + 1.
D. 1 - e.
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = ex và trục y = 1 là: ex = 1 ⇔ x = 0
Do đó:
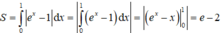
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
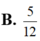
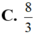
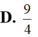
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
A . 37 12
B . 5 12
C . 8 3
D . 9 4
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
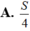
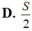
Tính diện tích hình phẳng giới hạn bởi các đường y = x 2 + x - 1 và y = x 4 + x - 1 là:
A. 4 15
B. 15 4
C. 4,15
D. 4,05
Phương trình hoành độ giao điểm của hai đường cong là
x 2 + x - 1 = x 4 + x - 1 ⇔ x 2 - x 4 = 0 ⇔ x ∈ 0 ; 1 ; - 1
Khi đó diện tích cần tìm là
S = ∫ - 1 1 x 2 - x 4 d x = ∫ - 1 0 x 2 - x 4 d x + ∫ 0 1 x 2 - x 4 d x = x 3 3 - x 5 5 - 1 0 + x 3 3 - x 5 5 0 1 = 4 15
Đáp án A
Diện tích hình phẳng được giới hạn bởi các đường y = x 2 + x - 1 v à y = x 4 + x - 1 là:
A. 8 15 d v t t
B. 7 15 d v t t
C. - 7 15 d v t t
D. 4 15 d v t t
Chọn D.
Phương trình hoành độ giao điểm của đồ thị hàm số y = x2 + x - 1 và y = x4 + x - 1 là :
