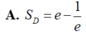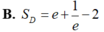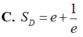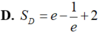Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = ex và trục y = 1 là: ex = 1 ⇔ x = 0
Do đó:
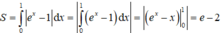
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = ex và trục y = 1 là: ex = 1 ⇔ x = 0
Do đó:
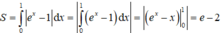
Diện tích hình phẳng được giới hạn bởi các đường y = ln x, x = 1/e, x = e và trục hoành là
A. 1 - 1 e
B. 2 1 + 1 e
C. 2 1 - 1 e
D. 1 + 1 e
Tính diện tích các hình phẳng giới hạn bởi các đường sau: y = x - 1 + lnx x , y = x - 1 và x = e
Tính diện tích S của hình phẳng giới hạn bởi các đường y = ex, y = e–x, x = 1.
A. S = e + 1 2 - 2
B. S = e - 1 e - 2
C. S = e + 1 e
D. S = e + 1 e - 2
Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) y = 2x – x 2 , x + y = 2 ;
b) y = x 3 – 12x, y = x 2
c) x + y = 1, x + y = -1, x – y = 1, x – y = -1;
d) 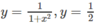
e) y = x 3 – 1 và tiếp tuyến với y = x 3 – 1 tại điểm (-1; -2).
Diện tích hình phẳng giới hạn bởi các đường y = 1 + ln x x , y=0, x=1 và x=e là S = a 2 + b . Khi đó giá trị a 2 + b 2 là:
A. 2 3
B. 4 3
C. 20 9
D. 2
Tính diện tích hình phẳng giới hạn bởi các đường y = ( e + 1 ) x y = ( e x + 1 ) x Chọn đáp án đúng:
![]()
![]()

Diện tích hình phẳng giới hạn bởi y = ( e + 1 ) x và y = ( 1 + e x ) x là:
A. 1 - e 2
B. e 2 - 1
C. e - 1
D. 1 - e
Diện tích hình phẳng được giới hạn bởi đồ thi hàm số y = ex – e–x, trục hoành, trục tung và đường thẳng x = –1, x = 1 là:
A. 2 e + 1 e - 2
B. 2 e - 1 e - 2
C. 2 e + 1 e + 2
D. 2 e - 1 e - 1
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = e x - e - x , trục hoành, đường thẳng x = -1 và đường thẳng x = 1.
A. e + 1 e - 2
B. 0
C. 2 e + 1 e - 2
D. e + 1 e
Tính diện tích Sd của miền phẳng D giới hạn bởi y= e x ; y = e - x ; và x=1