Các câu hỏi tương tự
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng
y
ln
x
;
y
0
;
x
1
;
x
e
A. e - 2 B. e + 2 C.
π
(
e
+
2
)
D.
π
(
e...
Đọc tiếp
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng y = ln x ; y = 0 ; x = 1 ; x = e
A. e - 2
B. e + 2
C. π ( e + 2 )
D. π ( e - 2 )
Tính diện tích giới hạn bởi các đường cong y (x - 1)lnx và y x - 1. A.
e
2
-
4
e
+
5
4
B.
3
e
2
-
2
e
+...
Đọc tiếp
Tính diện tích giới hạn bởi các đường cong y = (x - 1)lnx và y = x - 1.
A. e 2 - 4 e + 5 4
B. 3 e 2 - 2 e + 5 2
C. 7 e 2 - e + 2 3
D. 4 e 2 + 3 e - 2 5
Tính diện tích hình phẳng giới hạn bởi các đường sau: x + y = 1, x + y = -1, x – y = 1, x – y = -1
Tính diện tích S của hình phẳng giới hạn bởi các đường y ex, y e–x, x 1. A.
S
e
+
1
2
-
2
B.
S
e
-
1
e
-
2
C.
S
e
+
1
e...
Đọc tiếp
Tính diện tích S của hình phẳng giới hạn bởi các đường y = ex, y = e–x, x = 1.
A. S = e + 1 2 - 2
B. S = e - 1 e - 2
C. S = e + 1 e
D. S = e + 1 e - 2
Tính diện tích các hình phẳng giới hạn bởi các đường sau: y = x 3 - x 2 và y = 1 9 (x - 1)
Tính diện tích hình phẳng giới hạn bởi các đường
y
(
e
+
1
)
x
y
(
e
x
+
1
)
x
Chọn đáp án đúng:
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi các đường y = ( e + 1 ) x y = ( e x + 1 ) x Chọn đáp án đúng:
![]()
![]()

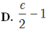
Tính diện tích của hình phẳng giới hạn bởi các đường sau: y = | x 2 – 1| và y = 5 + |x|
Thể tích khối tròn xoay sinh bởi hình phẳng (H) quay quanh trục Ox biết hình (H) giới hạn bởi các đường y lnx; y x; x1;
x
e
2
là:
Đọc tiếp
Thể tích khối tròn xoay sinh bởi hình phẳng (H) quay quanh trục Ox biết hình (H) giới hạn bởi các đường y = lnx; y =x; x=1; x = e 2 là:
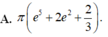
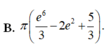
![]()
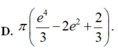
Diện tích hình phẳng được giới hạn bởi các đường y ln x, x 1/e, x e và trục hoành là A.
1
-
1
e
B.
2
1
+
1
e
C.
2
1
-
1...
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi các đường y = ln x, x = 1/e, x = e và trục hoành là
A. 1 - 1 e
B. 2 1 + 1 e
C. 2 1 - 1 e
D. 1 + 1 e



