Phần II: Tự luận
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD. Tìm giao tuyến của các mặt phẳng: d 1 = S A B ∩ S C D
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD. Tìm giao tuyến của các mặt phẳng: d 2 = S C D ∩ M A B
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)
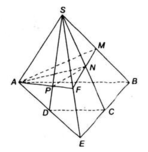
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
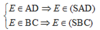
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) ?
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN) ?
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN) ?
a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.
(a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.
(b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
(c) Lấy một điểm K trên đoạn SE và gọi C' = SC ∩KB, D'=SD ∩KA. Chứng minh rằng hai giao điểm của AC' và BD' thuộc đường thẳng d nói trên.
a) Gọi N là giao điểm của EM và CD
Vì M là trung điểm của AB nên N là trung điểm của CD (do ABCD là hình thang)
⇒ EN đi qua G
⇒ S, E, M, G ∈ (α) = (SEM)
Gọi O là giao điểm của AC và BD
Ta có (α) ∩ (SAC) = SO
và (α) ∩ (SBD) = SO = d
b) Ta có: (SAD) ∩ (SBC) = SE
c) Gọi O' = AC' ∩ BD'
Ta có AC' ⊂ (SAC), BD' ⊂ (SBD)
⇒ O' ∈ SO = d = (SAC) ∩ (SBD)
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là trung điểm của các cạnh SB. a) Tìm giao tuyến của mặt phẳng (SAD) với mặt phẳng (SBC)? b) Tìm giao tuyến I của đường thẳng DM với (SAC)? c) Tìm thiết diện của mặt phẳng (MDC) với hình chóp S.ABCD?
a.
Trong mp (ABCD), kéo dài AD và BC cắt nhau tại E
\(\left\{{}\begin{matrix}E\in AD\in\left(SAD\right)\\E\in BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow E\in\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow SE=\left(SAD\right)\cap\left(SBC\right)\)
b.
Gọi O là giao điểm AC và BD \(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (SBD), nối DM cắt SO tại I
\(\left\{{}\begin{matrix}I\in SO\in\left(SAC\right)\\I\in DM\end{matrix}\right.\)
\(\Rightarrow I=DM\cap\left(SAC\right)\)
c.
Gọi F là trung điểm SA \(\Rightarrow FM\) là đường trung bình tam giác SAB
\(\Rightarrow FM||AB\Rightarrow FM||CD\)
Mà \(M\in\left(MCD\right)\Rightarrow F\in\left(MCD\right)\)
\(\Rightarrow\) Tứ giác CDFM là thiết diện của (MCD) và chóp
Cho hình chóp S.ABCD đáy là hình thang có đáy lớn là AB, đáy nhỏ là CD. Lấy 1 điểm bất kì trên SD . Tìm giao tuyến của
( SAC ) giao ( MBC)
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28)
a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).
b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.
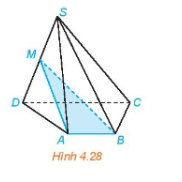
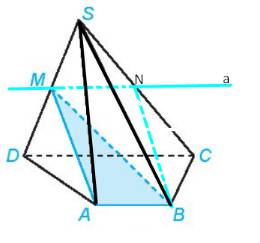
a) mp(MAB) và (SCD)có điểm M chung và chứa hai đường thẳng thẳng song song là AB và CD
Do đó giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng a đi qua M và song song với CD, AB.
b, Do MN //CD và M là trung điểm của SD.
Suy ra, MN là đường trung bình của tam giác SCD.
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AD. Gọi H,K lần lượt là trung điểm SB, SD, I = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
a: \(I\in BD\subset\left(SBD\right)\)
\(I\in AC\subset\left(SAC\right)\)
Do đó: \(I\in\left(SBD\right)\cap\left(SAC\right)\)
mà \(S\in\left(SBD\right)\cap\left(SAC\right)\)
nên \(\left(SBD\right)\cap\left(SAC\right)=SI\)
b: Gọi K là giao của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
c: AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: \(\left(SAD\right)\cap\left(SBC\right)=xy\), xy đi qua S và xy//AD//BC
Cho hình chóp S.ABCD có đáy ABCD là hình thang,AB là đáy lớn,O là giao điểm của AC và BD. Gọi M,N lần lược là trung điểm của SB và SD a) Chứng minh CD // (SAB) b) Tìm giao tuyến của hai mặt phẳng (CMN) và (ABCD) c) Gọi P là trung điểm của SC, I là giao điểm của OP và (CMN). Tính tỉ số IP/IO
a: Ta có: CD//AB
AB\(\subset\)(SAB)
CD không nằm trong mp(SAB)
Do đó: CD//(SAB)
b: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình của ΔSBD
=>MN//BD
Xét (CMN) và (ABCD) có
\(C\in\left(CMN\right)\cap\left(ABCD\right)\)
MN//BD
Do đó: (CMN) giao (ABCD)=xy, xy đi qua C và xy//MN//BD