Cho log a x = p ; log b x = q ; log a b c x = r . Hãy tính log c x theo p, q, r
A. log c x = 1 r - 1 p - 1 q
B. log c x = 1 1 r + 1 p + 1 q
C. log c x = 1 1 r - 1 p - 1 q
D. log c x = 1 r + 1 p + 1 q
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
1)Cho X = log\(\dfrac{1}{2}\)+log\(\dfrac{2}{3}\)+...+log\(\dfrac{99}{100}\). Chọn câu trả lời đúng về giá trị của X:
a)X>2 b)X=0 c) X=-2 d)X=\(\dfrac{1}{2}\)
2)Đặt log32 =a ,log35 = b. X=log3\(\dfrac{1}{2}\)+log3\(\dfrac{2}{3}\)+....+log3\(\dfrac{99}{100}\). X được biểu thị qua a,b là:
a) X=-2a-2b b)X =-2a+2b
c)X =2a-2b c)X =2a+2b
1) X=log1-log2+log2-log3+...+log99-log100
=log1-log100
=0-2
=-2
Đáp án C
2)X=-log3100=-log3102=-2log3(2.5)=-2log32-2log35=-2a-2b
Đáp án A
Cho đồ thị ba hàm số \(y = {\log _a}x,y = {\log _b}x\) và \(y = {\log _c}x\) như hình bên. Mệnh đề nào sau đây là đúng?
A. \(a > b > c\).
B. \(b > a > c\).
C. \(a > b > c\).
D. \(b > c > a\).
Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)
\(log_cx\) nghịch biến biến nên 0<c<1
\(log_ax;log_bx\) đồng biến nên a>1; b>1
=>Loại D
\(log_ax>log_bx\left(x>1\right)\)
=>\(\dfrac{1}{log_xa}< \dfrac{1}{log_xb}\)
=>a<b
=>Chọn B
Nếu log cơ số a của x=1/2 log cơ số a của 9 -log cơ số a của 5+ log cơ số a của 2 ( a>0. a#1) thì x =?
1. cho a=log3 2 và b=log3 5. tính các logarit sau theo a, b; A=log3 80, B=log3 37,5
2. cho log10 3=a, log5=b. tính C=log30 8 theo a, b
3. cho log27 5=a, log8 7=b, log2 3=c. tính D log6 35 theo a, b, c
Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)
Bài 3:
\(\log_{27}5=a; \log_87=b; \log_23=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln 27}=a; \frac{\ln 7}{\ln 8}=b; \frac{\ln 3}{\ln 2}=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln (3^3)}=a; \frac{\ln 7}{\ln (2^3)}=b; \ln 3=c\ln 2\)
\(\Leftrightarrow \frac{\ln 5}{3\ln 3}=a; \frac{\ln 7}{3\ln 2}=b; \ln 3=c\ln 2\)
\(\Rightarrow \frac{\ln 5}{3c\ln 2}=a; \frac{\ln 7}{3\ln 2}=b\)
\(\Rightarrow \ln 35=\ln 5+\ln 7=3ac\ln 2+3b\ln 2\)
Do đó:
\(D=\log_6 35=\frac{\ln 35}{\ln 6}=\frac{\ln 35}{\ln 2+\ln 3}=\frac{\ln 35}{\ln 2+c\ln 2}=\frac{3ac\ln 2+3b\ln 2}{\ln 2+c\ln 2}\)
\(=\frac{3ac+3b}{1+c}\)
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
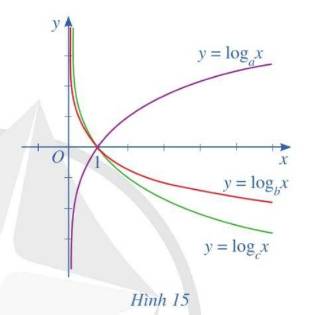
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Cho x, y > 0 thỏa mãn log(x + 2y) = log x + log y. Khi đó, giá trị nhỏ nhất của biểu thức
P = x 2 1 + 2 y + 4 y 2 1 + x là:
A. 6
B. 32 5
C. 31 5
D. 29 5
Đáp án B
Ta có log(x + 2y) = log x + log y
<=> log 2 (x+2y) = log 2xy
<=> 2 (x+2y) = 2xy (*).
Đ ặ t a = x > 0 b = 2 y > 0 , khi đó
* ⇔ 2 a + b = a b
và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .
Đặt t = a + b, do đó
P ≥ f t = t 2 t + 2 .
X é t h à m s ố f t = t 2 t + 2 t r ê n [ 8 ; + ∞ )
c ó f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8
Suy ra f(t) là hàm số đồng biến trên [ 8 ; + ∞ )
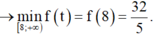
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .
Cho : log\(_x\) = \(\sqrt{2}\)
Tính biểu thức A = log\(_2x^3\) + log\(_{\frac{1}{2}x^3}\) + log\(_4x\)
loga4 X - loga2 X +logaX=\(\frac{3}{4}\) với 0<a khác 1
ĐKXĐ: \(x>0\)
\(log_{a^4}x-log_{a^2}x+log_ax=\frac{3}{4}\)
\(\Leftrightarrow\frac{1}{4}log_ax-\frac{1}{2}log_ax+log_ax=\frac{3}{4}\)
\(\Leftrightarrow\frac{3}{4}log_ax=\frac{3}{4}\)
\(\Leftrightarrow log_ax=1\)
\(\Rightarrow x=a\)