Giúp mình câu 13 di

Những câu hỏi liên quan
 Giúp mình mình câu 12 và 13
Giúp mình mình câu 12 và 13
Câu 12:
C5H12 → C5H11Cl
CTCT: \(CH_3CH_2CH_2CH_2CH_2Cl\)
\(CH_3CHClCH_2CH_2CH_3\)
\(CH_3CH_2CHClCH_2CH_3\)
→ Đáp án: C.
Câu 13:
Gọi CTPT của X là CnH2n.
Ta có: \(n_{C_2H_6}.30+n_X.14n=14,6\left(1\right)\)
m bình tăng = mX = 5,6 (g) = nX.14n (2)
Từ (1) và (2) \(\Rightarrow n_{C_2H_6}.30+5,6=14,6\Rightarrow n_{C_2H_6}=0,3\left(mol\right)\)
Mà: Thể tích hh A giảm đi 1/4
\(\Rightarrow\dfrac{V_X}{V_X+V_{C_2H_6}}=\dfrac{1}{4}\Rightarrow\dfrac{n_X}{n_X+n_{C_2H_6}}=\dfrac{1}{4}\Rightarrow n_X=0,1\left(mol\right)\)
Thay vào (2), được n = 4.
Vậy: X là C4H8.
→ Đáp án: D
Đúng 1
Bình luận (0)
Mn làm và giải thích giúp mình trừ câu 13 ,15,18 cong mấy câu kia mn giải thích giúp mình nha
Giúp mình câu 10 câu 13 14 15
10/13<.../22<11/13 ai giúp mình câu này
Lời giải:
$\frac{10}{13}< \frac{....}{22}< \frac{11}{13}$
$\Rightarrow \frac{220}{286}< \frac{13\times ....}{286}< \frac{242}{286}$
$\Rightarrow 220< 13\times .....< 242$
$\Rightarrow \frac{220}{13}< ....< \frac{242}{13}$
$\Rightarrow 16,92...< .....< 18,62....$
$\Rightarrow ....$ có thể nhận giá trị 17 hoặc 18.
Đúng 3
Bình luận (0)
Giúp mình từ câu 8 đến câu 13 với
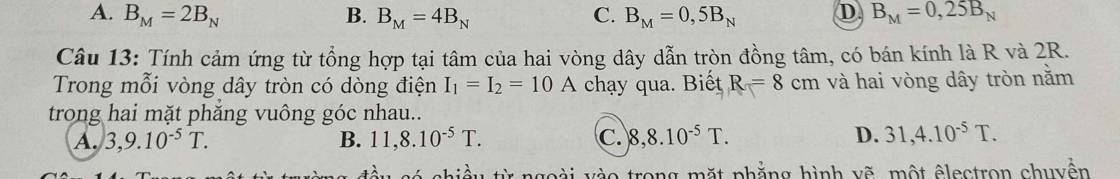 Giúp mình câu 13
Giúp mình câu 13
Giúp mình câu này : Nêu các bước Di chuyển trên trang tính ?
Các bước di chuyển nội dung ô tính :
B1 : Chọn ô hoặc các ô có dữ liệu ta muốn di chuyểnB2 : Nháy nút Cut trên thanh công cụ B3 : Chọn ô ta muốn đưa dữ liệu đc di chuyển tới B4 : Nháy nút Paste trên thanh công cụ
Đúng 0
Bình luận (0)
GIÚP MÌNH 3 CÂU: CÂU 8, 12 VỚI 13 THÔI Ạ!!
8 disappointing
12 preservation
13 seriously
Đúng 3
Bình luận (0)
Cho tam giác DEF vuông góc tại D,DI là đường cao,DE=9 cm,EF=13 cm
a.Giải tam giác DEF.
b.Tính DI,IE,IF
c.Kẻ IM vuông góc DE,IN vuông góc DF.Tính MN và chứng minh DE.DM=DF.DN.
Trả lời giúp mình với ạ!Mình cảm ơn nhiều!
a) Áp dụng định lí Pytago vào ΔEDF vuông tại D, ta được:
\(EF^2=DF^2+DE^2\)
\(\Leftrightarrow DF^2=13^2-9^2=88\)
hay \(DF=2\sqrt{22}\left(cm\right)\)
Xét ΔEDF vuông tại D có
\(\sin\widehat{E}=\dfrac{DF}{EF}=\dfrac{2\sqrt{22}}{13}\)
nên \(\widehat{E}\simeq46^0\)
\(\Leftrightarrow F=44^0\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔDFE vuông tại D có DI là đường cao ứng với cạnh huyền EF, ta được:
\(DI\cdot EF=DF\cdot DE\)
\(\Leftrightarrow DI=\dfrac{18\sqrt{22}}{13}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔDIF vuông tại I, ta được:
\(DF^2=DI^2+IF^2\)
\(\Leftrightarrow IF^2=DF^2-DI^2=\left(2\sqrt{22}\right)^2-\left(\dfrac{18\sqrt{22}}{13}\right)^2=\dfrac{7744}{169}\)
hay \(IF=\dfrac{88}{13}\left(cm\right)\)
Ta có: IE+IF=EF(I nằm giữa E và F)
nên \(IE=EF-IF=13-\dfrac{88}{13}=\dfrac{81}{13}\left(cm\right)\)
Đúng 3
Bình luận (0)
c) Xét tứ giác DMIN có
\(\widehat{NDM}=90^0\)
\(\widehat{IND}=90^0\)
\(\widehat{IMD}=90^0\)
Do đó: DMIN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: DI=MN(Hai đường chéo của hình chữ nhật DMIN)
mà \(DI=\dfrac{18\sqrt{22}}{13}\left(cm\right)\)
nên \(MN=\dfrac{18\sqrt{22}}{13}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDIE vuông tại I có IM là đường cao ứng với cạnh huyền DE, ta được:
\(DM\cdot DE=DI^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDIF vuông tại I có IN là đường cao ứng với cạnh huyền DF, ta được:
\(DN\cdot DF=DI^2\)(2)
Từ (1) và (2) suy ra \(DM\cdot DE=DN\cdot DF\)
Đúng 2
Bình luận (0)























