Tìm tất cả các giá trị thực của tham số m để f(x) = m(x - m) - (x - 1) không âm với mọi x ∈ (- ∞ ; m + 1].
A. m = 1
B. m > 1
C. m < 1
D. m ≥ 1
1/ tìm tham số thực m để tồn tại x thỏa mãn f(x) = m^2x + 3 - ( mx + 4 ) âm. 2/ tìm tất cả các giá trị của m để f (x) = m( x-m ) - ( x - 1 ) không âm với mọi x thuộc ( - vô cực , m+1)
a) Tìm tất cả các giá trị của tham số m để \(g\left(x\right)=4mx^2-4\left(m-1\right)x+m-3\) luôn luôn âm với mọi x thuộc R
b) Tìm tất cả các giá trị của tham số m để \(f\left(x\right)=x^2-2\left(m+2\right)x-2m^2+3m+4\) không âm với mọi m thuộc R
c) Bất pt \(x^2+2mx+m^2-5m+6>0\) ( m là tham số thực) có nghiệm với mọi x thuộc R khi \(m\in\left(-\infty;\dfrac{a}{b}\right)\) với \(a,b\in Z\) và \(\dfrac{a}{b}\) là phân số tối giản. Tính giá trị biểu thức a+2b
a) Tam thức \(f\left(x\right)=x^2+2\left(m-1\right)+m^2-3m+4\) không âm với mọi giá trị x
b) Có bao nhiêu giá trị nguyên của tham số m để mọi x thuộc R biểu thức \(f\left(x\right)=x^2+\left(m+2\right)x+8m+1\) luôn nhận giá trị dương
c) Tìm tất cả các giá trị m để biểu thức \(f\left(x\right)=x^2+\left(m+1\right)x+2m+7>0\forall x\in R\)
tìm tất cả các giá trị m để f(x)= m(x -m) - (x -1) không âm với mọi x thuộc ( vô cực , m + 1 )
Tìm tất cả các giá trị thực của tham số m để hàm số f ( x ) = sin x - m sin 2 x - 1 3 sin 3 x + 2 m x có f ' ( x ) ≥ 0 với mọi x ∈ ℝ .
A. m ∈ [ 1 ; + ∞ )
B. m ∈ - 1 ; 1
C. m ∈ ( - ∞ ; - 1 ]
D. m ∈ 1 ; 2
Đáp án A.
Ta có f ' ( x ) = = cos x - 2 m cos 2 x - cos 3 x + 2 m = cos x - cos 3 x - 2 m ( cos 2 x - 1 )
Hàm số có f ' ( x ) ≥ 0 , ∀ x ∈ ℝ ⇔ cos x - cos 3 x ≥ 2 m cos 2 x - 1 , ∀ x ∈ ℝ . (*)
Với cos 2 x = 1 thì thỏa mãn (*).
Với cos 2 x ≢ 1 thì ⇔ cos x - cos 3 x cos 2 x - 1 ≤ 2 m , ∀ x ∈ ℝ .
Đặt cos x - cos 3 x cos 2 x - 1 = g ( x ) . Để g ( x ) ≤ 2 m , ∀ x ∈ ℝ , thì 2 m ≥ m a x R g ( x ) .
Sử dụng máy tính cầm tay ta có
![]()
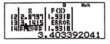
Từ bảng giá trị kết hợp với phương án thì ta suy ra
m a x ℝ g ( x ) = 2 ⇔ 2 m ≥ 2 ⇔ m ≥ 1 .
Tìm các giá trị thực của tham số m để f(x) = -x² -2(m-2)x +m+3 luôn âm với mọi x thuộc R
\(\Delta=\left(-2m+4\right)^2-4\cdot\left(-1\right)\left(m+3\right)\)
=4m^2-16m+16+4(m+3)
=4m^2-16m+16+4m+12
=4m^2-12m+28
Để f(x)<0 với mọi x thì 4m^2-12m+28<0 và -1<0
=>\(m\in\varnothing\)
a) Tìm tất cả các tham số m nguyên để \(F\left(x\right)=\dfrac{7}{x^2+\dfrac{1}{2}m}\) có nghiệm x nguyên và F(x) là số nguyên dương.
b) Với mọi \(m\ge0\), tìm giá trị lớn nhất của F(x).
Với mọi m < 0, tìm giá trị nhỏ nhất của F(x).
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Cho hàm số f(x) = x4 - 2x2 + m - 1 (với m là tham số thực). Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số g(x) = \(\left|f\left(x\right)\right|\) trên đoạn [0;2] bằng 2020.
\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Để \(g\left(x\right)_{min}>0\Rightarrow f\left(x\right)=0\) vô nghiệm trên đoạn đã cho
\(\Rightarrow\left[{}\begin{matrix}-m< -2\\-m>7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -7\end{matrix}\right.\)
\(g\left(0\right)=\left|m-1\right|\) ; \(g\left(1\right)=\left|m-2\right|\) ; \(g\left(2\right)=\left|m+7\right|\)
Khi đó \(g\left(x\right)_{min}=min\left\{g\left(0\right);g\left(1\right);g\left(2\right)\right\}=min\left\{\left|m-2\right|;\left|m+7\right|\right\}\)
TH1: \(g\left(x\right)_{min}=g\left(0\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m-2\right|\le\left|m+7\right|\\\left|m-2\right|=2020\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{5}{2}\\\left|m-2\right|=2020\end{matrix}\right.\) \(\Rightarrow m=2022\)
TH2: \(g\left(x\right)_{min}=g\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m+7\right|\le\left|m-2\right|\\\left|m+7\right|=2020\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\dfrac{5}{2}\\\left|m+7\right|=2020\end{matrix}\right.\) \(\Rightarrow m=-2027\)