Cho tam giác ABC vuông tại A . Gọi M , N, P lần lượt là trung điểm của AB; AC và BC. Hỏi tứ giác AMPN là hình gì? Chọn khẳng định đúng nhất?
A. Hình bình hành
B. Hình thang cân
C. Hình thang vuông
D. Hình chữ nhật
Những câu hỏi liên quan
22 tháng 9 2021 lúc 19:38
Bài 5: Cho tam giác ABC vuông tại A,AB12 cm BC13 cm .Gọi M, N lần lượt là trungđiểm của AB và BCa) Chứng minhMN vuông góc AB b) Tính độ dài MNBài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi Ilà giao điểm của AP và MN. C/m: a) IA IP b) IM IN.Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểmcủa DH, M là trung điểm của HC.C/m:a) IM vuông góc AD b) AI vuông góc DM.
Đọc tiếp
Bài 5: Cho tam giác ABC vuông tại A,
AB=12 cm BC=13 cm .
Gọi M, N lần lượt là trung
điểm của AB và BC
a) Chứng minh
MN vuông góc AB
b) Tính độ dài MN
Bài 6: Cho tam giác ABC; Gọi M, N, P lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi I
là giao điểm của AP và MN. C/m: a) IA = IP b) IM = IN.
Bài 7: Cho tam giác ABC cân tại A, đường cao AD, kẻ DH vuông góc AC. Gọi I là trung điểm
của DH, M là trung điểm của HC.
C/m:a) IM vuông góc AD b) AI vuông góc DM.
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB6m;AC8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 24HE mũ 2+4HD mũ 2
Đọc tiếp
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
Cho tam giác ABC vuông tại A có AB<AC. N là trung điểm BC. Gọi M, P lần lượt là hình chiếu của N trên AB, AC. Lấy E sao cho P là trung điểm của NE.
a) Chứng minh M,P lần lượt là trung điểm của AB, AC
b) Tứ giác ANCE là hình gì ( chứng minh hình)
a: Xét ΔCAB có
N là trung điểm của AB
NP//AB
=>P là trung điểm của AC
Xét ΔCAB có
N là trung điểm của BC
NM//AC
=>M là trung điểm của AB
b: Xét tứ giác ANCE có
P là trung điểm chung của AC và NE
AC vuông góc NE
=>ANCE là hình thoi
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm của ab ac bc. Gọi D, E lần lượt là điểm đối xứng của P qua M và N.a, Tính AP và diện tích tam giác ABC biết AB 6cm, AC 8cm.b, Chứng minh tứ giác AMPN là hình chữ nhật.c, Chúng minh tứ giác APCE là hình thoi.d, Tam giác ABC cần có điều kiện gì để tứ giác APCE là hình vuông?e, Chứng minh AP, BE, CD đồng quy.f, Chứng minh ba điểm D, A, E thẳng hàng.
Đọc tiếp
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm của ab ac bc. Gọi D, E lần lượt là điểm đối xứng của P qua M và N.
a, Tính AP và diện tích tam giác ABC biết AB = 6cm, AC = 8cm.
b, Chứng minh tứ giác AMPN là hình chữ nhật.
c, Chúng minh tứ giác APCE là hình thoi.
d, Tam giác ABC cần có điều kiện gì để tứ giác APCE là hình vuông?
e, Chứng minh AP, BE, CD đồng quy.
f, Chứng minh ba điểm D, A, E thẳng hàng.
cho tam giác ABC vuông cân tại A. gọi M,N lần lượt là trung điểm của AB và AC, kẻ NH vuông góc với CM tại H, HE vuông góc với AB tại E chứng minh tam giác ABH cân
bạn là fan j.fla hử. tui cũng thế nè
Cho tam giác ABC vuông tại A (AB AC). Gọi D và E lần lượt là trung điểm của BC và AC. a) Chứng minh tứ giác ABDE là hình thang vuôngCho tam giác ABC vuông tại A (AB AC). Gọi D và E lần lượt là trung điểm của BC và ACa) Chứng minh tứ giác ABDE là hình thang vuôngb) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬTc) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Gọi D và E lần lượt là trung điểm của BC và AC. a) Chứng minh tứ giác ABDE là hình thang vuôngCho tam giác ABC vuông tại A (AB < AC). Gọi D và E lần lượt là trung điểm của BC và AC
a) Chứng minh tứ giác ABDE là hình thang vuông
b) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬT
c) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
a) Chứng minh tứ giác ABDE là hình thang vuông
b) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬT
c) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
a: Xét ΔCAB có CE/CA=CD/CB
nên ED//AB và ED=AB/2
=>AEDB là hình thang
mà góc EAB=90 độ
nênAEDB là hình thang vuông
b: Xét tứ giác ABKC có
D là trung điểm chung của AK và BC
góc BAC=90 độ
Do đó: ABKC là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi D,E,F lần lượt là trung điểm của AB,AC,BC
a) So sánh diện tích tam giác ABC và tứ giác ADFE
b) Biết AB=6cm; BC=10cm.Gọi M,N,K lần lượt là trung điểm của DF,CD và DE. Tính diện tích MFNK
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính MN?
A. 4cm
B. 10cm
C. 5 cm
D. 7cm
Áp dụng định lí Pytago vào tam giác vuông ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10cm
Do M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra:
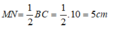
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, M là trung điểm của BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Gọi I, K lần lượt là trung điểm của MB, MC.
a) Tứ giác DIKE là hình gì
b) Tam giác ABC cần thêm điều kiện gì để DIKE là hình chữ nhật
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
ΔMDB vuông tại D có DI là trung tuyến
nên DI=MI=BI
ΔMEC vuông tại E có EK là trung tuyến
nên KC=KM=KE
Xét ΔABC có
M là trung điểm của BC
MD//AC
=>D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
=>E là trung điểm của AC
Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình
=>DE//BC và DE=BC/2
KI=KM+MI
=1/2(MC+MB)
=1/2BC
=DE
Xét tứ giác DIKE có
DE//KI
DE=KI
=>DIKE là hình bình hành
b: DIKE là hình chữ nhật
=>góc DIK=90 độ
=>DI vuông góc MB
Xét ΔDMB có
DI vừa là đường cao, vừa là đường trung tuyến
=>ΔDMB cân tại D
mà ΔDMB vuông cân tại D
nên góc B=45 độ
Đúng 1
Bình luận (1)
Bài 2. Cho tam giác ABC vuông tại A. Một đường thẳng song song với BC cắt hai cạnh AB vàAC lần lượt tại D và E. Gọi M và N lần lượt là trung điểm của DE và BC. Chứng minh rằng:a) Ba điểm A, M, N thẳng hàng;b) MN 2BC DEBài 3. Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HE AB; HF AC. Từ A vẽ mộtđường thẳng vuông góc với EF cắt BC tại M. Chứng minh rằng M là trung điểm của BC.
Đọc tiếp
Bài 2. Cho tam giác ABC vuông tại A. Một đường thẳng song song với BC cắt hai cạnh AB và
AC lần lượt tại D và E. Gọi M và N lần lượt là trung điểm của DE và BC. Chứng minh rằng:
a) Ba điểm A, M, N thẳng hàng;
b) MN =
2
BC DE
Bài 3. Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HE AB; HF AC. Từ A vẽ một
đường thẳng vuông góc với EF cắt BC tại M. Chứng minh rằng M là trung điểm của BC.
3:
Xét tứ giác AEHF có
góc AEH=góc AFH=góc EAF=90 độ
=>AEHF là hình chữ nhật
AM vuông góc EF
=>góc MAC+góc AFE=90 độ
=>góc MAC+góc AHE=90 độ
=>góc MAC+góc B=90 độ
mà góc MCA+góc B=90 độ
nên góc MAC=góc MCA
=>MA=MC
góc MAC+góc MAB=90 độ
góc MCA+góc MBA=90 độ
mà góc MAC=góc MCA
nên góc MAB=góc MBA
=>MA=MB
=>MB=MC
=>M là trung điểm của BC
Đúng 1
Bình luận (0)