Sử dụng tổng 3 góc trong tam giác( gợi ý chi tiết cx đc ạ)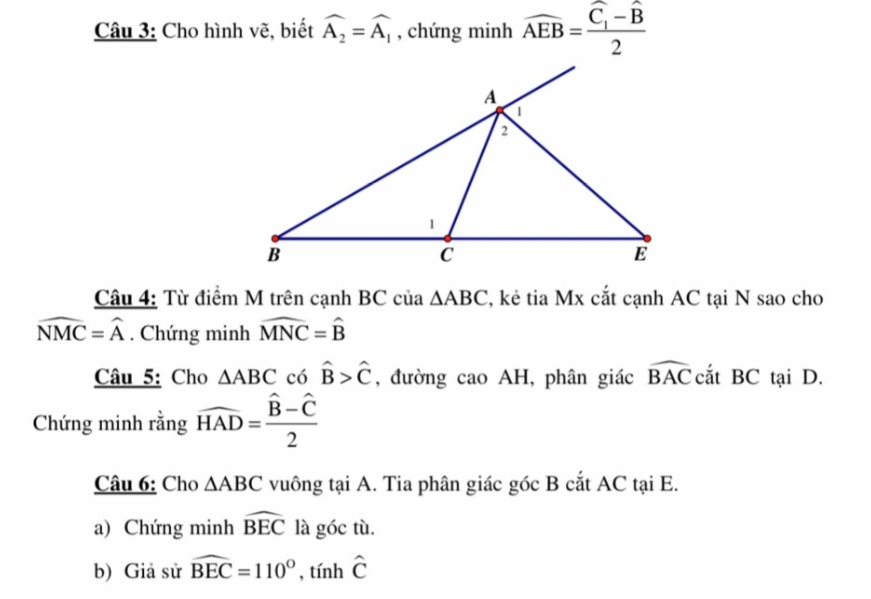

Những câu hỏi liên quan
Sử dụng tc góc trong, góc ngoài, tổng 3 góc tam giác ạ. Gợi ý cái nào lm trc cx đc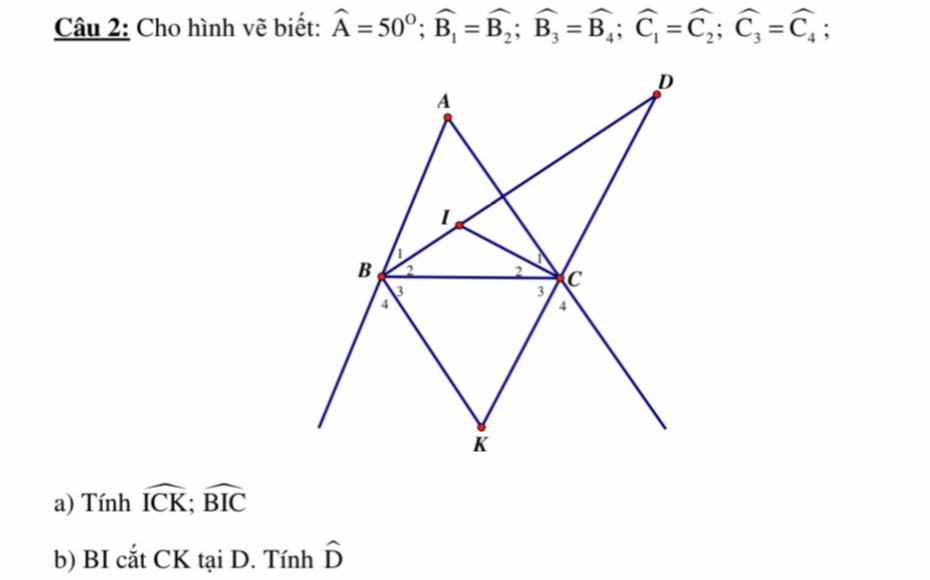
a. Gợi ý: \(\widehat{ICK}=\widehat{C_2}+\widehat{C_3}=\dfrac{1}{2}\left(\widehat{ACB}+\widehat{C}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
\(\widehat{BIC}=180^0-\left(\widehat{B_2}-\widehat{C_2}\right)=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\dfrac{1}{2}\left(180^0-\widehat{BAC}\right)=180^0-90^0+\dfrac{1}{2}\widehat{BAC}=90^0+25^0=115^0\)
b. \(\widehat{ICK}=\widehat{D}+\widehat{CID}\Rightarrow\widehat{D}=90^0-\widehat{CID}=90^0-\left(180^0-\widehat{BIC}\right)=...\)
Đúng 0
Bình luận (0)
Cho tam giác abc cân tại A, góc A bằng 20 độ, bc=2 cm. Tính AB
Gợi ý: sử dụng kiến thức tỉ số lượng giác góc nhọn trong tam giác vuông
Bạn tự vẽ hình nha
Từ A hạ AH vuông góc với BC
Ta có tam giác ABC là tam giác cân có
AH là đường cao
=>AH là đường phân giác và là đường trung trực
=>+)Góc BAH=Góc HAC = Góc BAC/2=20°/2=10°
+)HB=HC=BC/2=2/2=1
Theo tỉ số lượng giác trong tam giác AHB vuông tại H có:
Sin BAH=BH/AB
Sin10°=1/AB
<=>AB=1/Sin10°
<=> AB=5.76 cm
~Chúc bạn học tốt~
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD , AB=6cm ,AD=3cm, I là trung điểm của AB . CMR: DC là tia phân giác của góc ADC vẽ hình và giải chi tiết mình sẽ tick (gợi ý: áp dụng tam giác cân hoặc hình thoi)
Trình bày( sử dụng tổng 3 góc tam giác) ạ
Câu 1:
\(\left\{{}\begin{matrix}b-c=30\\b+c=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=70\\c=40\end{matrix}\right.\)
Vậy: ΔABC có hai góc bằng nhau
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Biết cosB = 0,8, hãy tính các tỉ số lượng giác của góc C.
Gợi ý: Sử dụng bài tập 14.
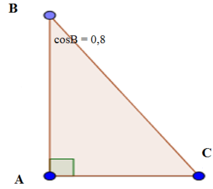
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
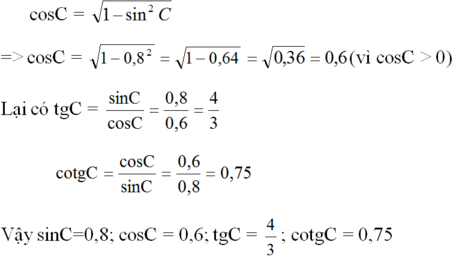
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Biết cosB = 0,8, hãy tính các tỉ số lượng giác của góc C.
Gợi ý: Sử dụng bài tập 14.
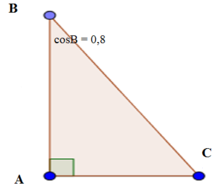
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
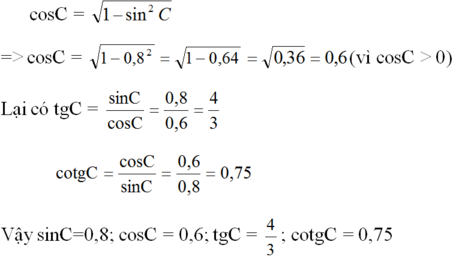
Đúng 0
Bình luận (0)
Cho tam giác ABC, tia phân giác góc BAC cắt tia phân giác góc ngoài tại C của tam giác ABC tại I. Chứng minh ABC=2AIC Gợi ý: Sử dụng tính chất góc ngoài tại đỉnh C của tam giác ABC và giác ngoài tại đỉnh C của tam giác AIC
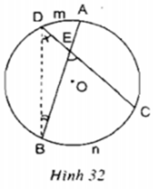
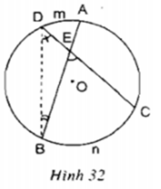
Hãy chứng minh định lý trên.Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B
E
C
^
s
đ
B
n
C
⏜
+
s
đ
A
m...
Đọc tiếp
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh: B E C ^ = s đ B n C ⏜ + s đ A m D ⏜ 2
Hãy chứng minh định lý trên.Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B
E
C
^
s
d
B
n
C
^
+
s
d
A
m
D
^...
Đọc tiếp
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B E C ^ = s d B n C ^ + s d A m D ^ 2