Giải các hệ phương trình
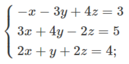
Nghiệm chung của ba phương trình đã cho được gọi là nghiệm của hệ gồm ba phương trình ấy. Giải hệ phương trình là tìm nghiệm chung của tất cả các phương trình trong hệ. Hãy giải các hệ phương trình sau: 3 x + 5 y = 34 4 x - 5 y = - 13 5 x - 2 y = 5

Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)
Nghiệm chung của ba phương trình đã cho được gọi là nghiệm của hệ gồm ba phương trình ấy. Giải hệ phương trình là tìm nghiệm chung của tất cả các phương trình trong hệ. Hãy giải các hệ phương trình sau: 6 x - 5 y = - 49 - 3 x + 2 y = 22 7 x + 5 y = 10

Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.
Giải các phương trình và hệ phương trình:

a)
`x^2+3x+2=0`
`<=>x^2+2x+x+2=0`
`<=>x(x+2)+(x+2)=0`
`<=>(x+2)(x+1)=0`
`<=>x+2=0` hoặc `x+1=0`
`<=>x=-2` hoặc `x=-1`
b)
\(\left\{{}\begin{matrix}x-3y=5\\3x+2y=4\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}3x-9y=15\\3x+2y=4\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}-11y=11\\x-3y=5\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}y=-1\\x-3\cdot\left(-1\right)=5\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}y=-1\\x=2\end{matrix}\right.\)
cho hệ phương trình
\(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y+1\end{matrix}\right.\)
a)giải hệ phương trình khi m=2
b)giải hệ phương trình theo m
c)tìm m để hệ có nghiệm (x;y) là các số dương
d)tìm m để hệ phương trình có nghiệm thỏa mãn x^2+y^2=1
Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$
Giải các bất phương trình và hệ phương trình sau
Gợi ý : Tìm đ/k của x trong căn thức
Xét 2 TH : x + 1 > 0 \(;x+1\le0\)
Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:
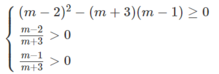
Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:
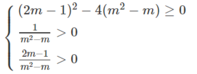
Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:
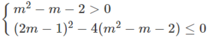
Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:
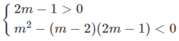
Giải các phương trình và hệ phương trình sau:
b) x 4 – 5x + 4 = 0
b) x 4 - 5 x 2 + 4 = 0
Đặt t = x 2 ≥ 0 , ta có phương trình:
t 2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t 1 = 1 (nhận) ; t 2 = 4 (nhận)
với t = 1 ⇔ x 2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x 2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2