Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O).
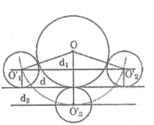
* Phân tích
- Giả sử dựng được đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O; 2cm).
- Đường tròn (O’; 1cm) tiếp xúc với d nên O’ cách d một khoảng bằng 1cm. Khi đó O’ nằm trên hai đường thẳng d 1 , d 2 song song với d và cách d một khoảng bằng 1cm.
- Đường tròn (O’; 1cm) tiếp xúc với đường tròn (O; 2cm) nên suy ra OO’ = 3cm. Khi đó O’ là giao điểm của (O; 3cm) với d 1 và d 2
* Cách dựng
- Dựng hai đường thẳng d 1 và d 2 song song với d và cách d một khoảng bằng 1cm.
- Dựng đường tròn (O; 3cm) cắt d 1 tại O ' 1 . Vẽ ( O ' 1 ; 1cm) ta có đường tròn cần dựng
* Chứng minh
Theo cách dựng, O ' 1 cách d một khoảng bằng 1cm nên (O’1; 1cm) tiếp xúc với d.
Vì O O ' 1 = 3cm nên ( O ' 1 ; 1cm) tiếp xúc với (O; 2cm)
* Biện luận: O các d 1 một khoảng bằng 1cm nên (O; 3cm) cắt d1 tại hai điểm phân biệt.
Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O';1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O) ?
cho hàm số y=x^2 có đồ thị là P . a, vẽ P . b, tìm K để đường thẳng (d) y=2x-K+1 tiếp xúc vớ
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+k-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\left(k-1\right)=-4k+4+4=-4k+8\)
Để (P) tiếp xúc với (d) thì -4k+8=0
hay k=2
Trong mặt phẳng tọa độ Oxy, cho đường tròn C 1 : x 2 + y 2 = 4 , C 2 : x 2 + y 2 - 12 x + 18 = 0 và đường thẳng d : x - y + 4 = 0 . Phương trình đường tròn có tâm thuộc C 2 , tiếp xúc với d và cắt C 1 tại hai điểm phân biệt A và B sao cho AB vuông góc với d là:
A. x - 3 2 + y - 3 2 = 4
B. x - 3 2 + y - 3 2 = 8
C. x + 3 2 + y + 3 2 = 8
D. x + 3 2 + y + 3 2 = 4
Trong mặt phẳng tọa độ Oxy, cho đường tròn ( C 2 ) : x 2 + y 2 - 12 x + 18 = 0 và đường thẳng d:x-y+4. Phương trình đường tròn có tâm thuộc ( C 2 ), tiếp xúc với d và cắt ( C 1 ) tại hai điểm phân biệt A và B sao cho AB vuông góc với d là
Cho 2 đường tròn (O;R) và (O'R') nằm ngoài nhau. Một đường thẳng d tiếp xúc trong với cả 2 đường tròn tại A,B. Một đường thẳng d' ≠ d tiếp xúc trong với cả 2 đường tròn tại C,D.
Cm: a) AB=CD.
b) Các đường thẳng AB,CD cắt nhau trên đường thẳng OO'
Cho đường tròn (O;2cm) tiếp xúc với đường thẳng d.Dựng đường tròn (O';1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O)
cho 2 đường tròn i và k tiếp xúc ngoài với nhau các đường tròn này tiếp xúc trong với o tại e và f. Dây BC của đường tròn o tiếp xúc với các đường tròn i và k lần lượt tại N và M . CM: D, N , E thẳng hàng , d , m ,f thẳng
Bài 12: Cho (P): \(y=\dfrac{x^2}{4}\)và đường thẳng (d) đi qua điểm I \(\left(\dfrac{3}{2};1\right)\) có hệ số góc là m
1. Vẽ (P) và viết Phương trình (d)
2. Tìm m sao cho (d) tiếp xúc (P)
3. Tìm m sao cho (d) và (P) có hai điểm chung phân biệt
