Đại lượng y trong bảng nào sau đây không phải là hàm số của đại lượng x tương ứng:
Hãy khoanh tròn chữ cái đứng trước câu trả lời đúng.
Đại lượng y trong bảng nào sau đây không phải là hàm số của đại lượng x tương ứng:
a)
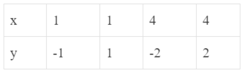
b)
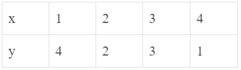
c)
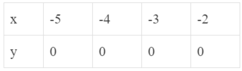
d)
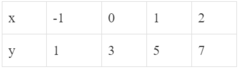
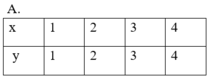
* Xét bảng A ta thấy:
+ Với x = 1 cho hai giá trị y tương ứng: y = -1 và y = 1.
+ Với x = 4 cho hai giá trị y tương ứng: y = -2 và y = 2
Do đó, đại lượng y trong bảng A không phải là hàm số của đại lượng x tương ứng.
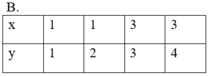
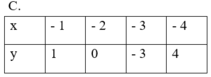
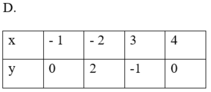
* Các bảng B, C và D đều thỏa mãn: Với mỗi giá trị của x ta chỉ xác định được đúng một giá trị tương ứng của y. Nên đại lượng y trong các bảng B, C và D đều là hàm số của đại lượng x.
Chọn A.
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.
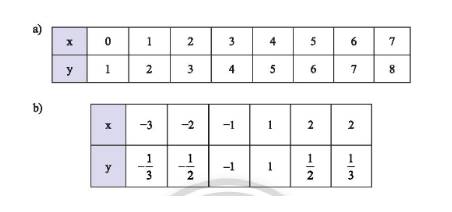
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).
Hãy khoanh tròn chữ cái đứng trước câu trả lời đúng
Đại lượng y trong bảng nào sau đây không phải là hàm số của đại lượng x tương ứng ?

Đại lượng y trong bảng A không phải là hàm số của đại lượng tương ứng.
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
| x | 4 | 4 | 9 | 16 |
| y | -2 | 2 | 3 | 4 |
Trong bảng ta thấy ứng với giá trị x = 4 có hai giá trị khác nhau của y là 2 và -2. Theo định nghĩa thì y không phải là hàm số của đại lượng x.
a) Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau:

Đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không?
b) Cho hàm số \(y = f\left( x \right) = {x^2}\)
- Tính \(f\left( 2 \right);f\left( { - 3} \right)\).
- Lập bảng giá trị của hàm số với \(x\) lần lượt bằng \( - 3; - 2; - 1;0;1;2;3\).
a) Đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ xác nhận được duy nhất một giá trị \(y\) tương ứng.
b) \(f\left( 2 \right) = {2^2} = 4;f\left( { - 3} \right) = {\left( { - 3} \right)^2} = 9\)
Ta có: \(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\(f\left( 0 \right) = {0^2} = 0;f\left( 1 \right) = {1^2} = 1\)
\(f\left( 2 \right) = {2^2} = 4;f\left( 3 \right) = {3^2} = 9\)
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(f\left( x \right)\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1 | 1 | 1 | 1 | 1 |
Trong bảng ta thấy ứng với mỗi giá trị của x ta luôn xác định được chỉ một giá trị của y. Theo định nghĩa thì y là hàm số của đại lượng x. Ở đây giá trị của y không đổi nên hàm số là hàm hằng.
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2 | 2 | 2 | 2 | 2 |
Vì mọi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là
| x | -3 | -2 | -1 | 1/2 | 1 | 2 |
| y | -5 | -7,5 | -15 | 30 | 15 | 7,5 |
Vì mọi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x
Các giá trị tương ứng của đại lượng x và y được cho bởi bảng sau:
1) x=-3,y=1
2) x=-8,y=5
3) x=-6,y=10
4)x=3,y=7
5) x=-2, y=9
6) x=-6, y=3
Đại lượng y có phải là hàm số của đại lượng x không ?Tại sao?
Đại lượng y là hàm số của đại lượng x. Bởi vì với mỗi giá trị của x chỉ tìm được duy nhất một giá trị tương ứng của y