Công thức nào sau đây là công thức thấu kính:

A.  1 d + d ' = 1 f

B.  1 f = 1 d + 1 d '

C.  1 d − d ' = 1 f

D.  1 f = 1 d − 1 d '

Công thức nào sau đây là công thức thấu kính:

A. 1 d + d ' = 1 f  

B. 1 f = 1 d + 1 d '

C. 1 d - d ' = 1 f

D. 1 f = 1 d - 1 d '

Công thức nào sau đây là công thức thấu kính?

A. 1 f = 1 d + 1 d '

B. 1 d + d ' = 1 f

C. 1 d - d ' = 1 f

D. 1 f = 1 d - 1 d '

Công thức nào sau đây là công thức thấu kính?

A.  1 f = 1 d + 1 d '

B.  1 d + d ' = 1 f

C.  1 d - d ' = 1 f

D.  1 f = 1 d - 1 d '

Gọi D là độ tụ của một thấu kính mỏng; d, d' là khoảng cách từ thấu kính đến vật và đến ảnh. Công thức nào dưới đây là đúng

A. D =  d d ' d + d '             C. D =  d + d ' d d '

B. D =  d d ' d - d '             D. D =  d - d ' d d '

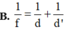
Công thức nào sau đây dùng để xác định vị trí ảnh của vật tạo bởi thấu kính?

A. d = f 

B. 1 f = 1 d + 1 d '

C. 1 f + 1 d = 1 d '

D. d = - d

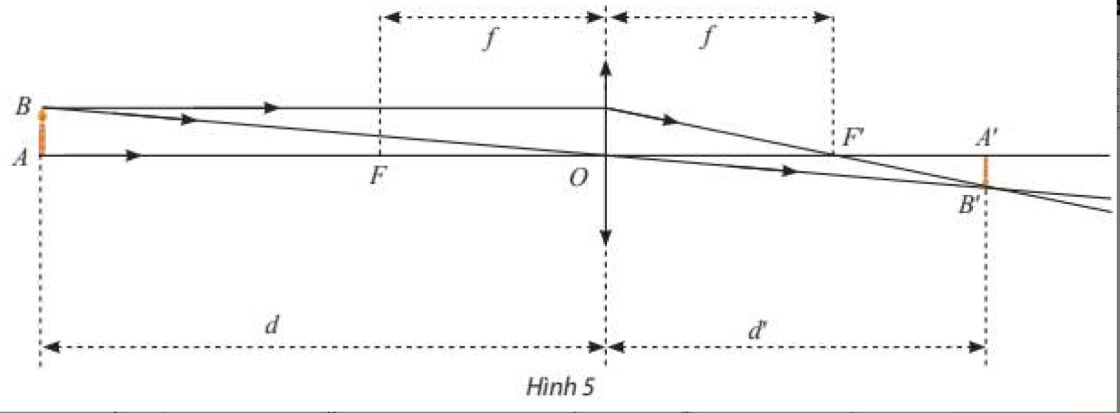
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) hay \(d' = \frac{{df}}{{d - f}}\).

Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.

a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);        

b) \(\mathop {\lim }\limits_{d \to  + \infty } g\left( d \right)\).