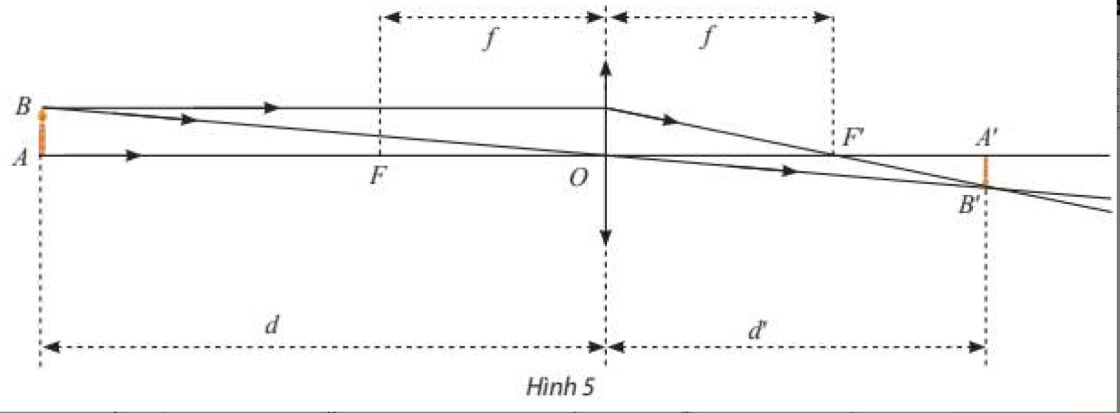
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) hay \(d' = \frac{{df}}{{d - f}}\).
Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right)\).
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)
Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} = + \infty \)
\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \)
Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)
Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F'} \right)\).



