Nối các điểm để có:
a) Một hình vuông

Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
a) Kí hiệu \({a_n}\) là diện tích của hình vuông thứ \(n\) và \({S_n}\) là tổng diện tích của \(n\) hình vuông đầu tiên. Viết công thức tính \({a_n},{S_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {S_n}\) (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).
b) Kí hiệu \({p_n}\) là chu vi của hình vuông thứ \(n\) và \({Q_n}\) là tổng chu vi của \(n\) hình vuông đầu tiên. Viết công thức tính \({p_n}\) và \({Q_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {Q_n}\) (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).

a) Gọi \({u_n}\) là độ dài cạnh của hình vuông thứ \(n\).
Ta có: \({u_1} = 1;{u_2} = \frac{{{u_1}}}{2}.\sqrt 2 = \frac{{{u_1}}}{{\sqrt 2 }};{u_3} = \frac{{{u_2}}}{2}.\sqrt 2 = \frac{{{u_2}}}{{\sqrt 2 }};...\)
Từ đó ta thấy \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \({u_n} = {u_1}.{q^{n - 1}} = 1.{\left( {\frac{1}{{\sqrt 2 }}} \right)^{n - 1}} = \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Diện tích của hình vuông thứ \(n\) là: \({a_n} = u_n^2 = {\left( {\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)^2} = \frac{1}{{{2^{n - 1}}}},n = 1,2,3,...\)
Vậy \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}}\)
Đây là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\).
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = 2\left( {1 - \frac{1}{{{2^n}}}} \right)\).
\(\lim {S_n} = \lim 2\left( {1 - \frac{1}{{{2^n}}}} \right) = 2\left( {1 - \lim \frac{1}{{{2^n}}}} \right) = 2\left( {1 - 0} \right) = 2\).
b) Chu vi của hình vuông thứ \(n\) là: \({p_n} = 4{u_n} = 4.\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Vậy \({Q_n} = 4 + \frac{4}{{\sqrt 2 }} + \frac{4}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 4\left( {1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)\)
\(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}\) là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 1.\frac{{1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^n}}}{{1 - \frac{1}{{\sqrt 2 }}}} = \left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\).
\( \Rightarrow {Q_n} = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\)
\(\begin{array}{l}\lim {Q_n} = \lim 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right) = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\\ & = 4\left( {2 + \sqrt 2 } \right)\left( {1 - 0} \right) = 4\left( {2 + \sqrt 2 } \right)\end{array}\).
Nối các điểm để có một hình vuông và hai hình tam giác.

Phương pháp giải:
- Nối các điểm đã cho, đếm số hình vuông và hình tam giác tạo thành.
- Nếu bằng với số lượng đề bài yêu cầu thì đó là cách vẽ cần tìm.
Lời giải chi tiết:
Nối các điểm để có:
b) Một hình vuông và hai hình tam giác

Một hình vuông \({C_1}\) có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thàng bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông \({C_2}\) (Hình 4). Từ hình vuông \({C_2}\) lại làm tiếp tục như trên để có hình vuông \({C_3}\). Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông \({C_1},{C_2},{C_3},..,{C_n},...\). Gọi \({a_n}\) là độ dài cạnh hình vuông \({C_n}\). Chứng minh rằng dãy số \(\left( {{a_n}} \right)\) là cấp số nhân.
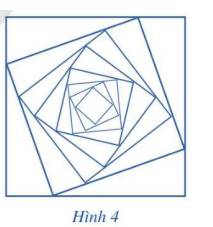
Ta có độ dài cạnh các hình vuông \({C_1},{C_2},{C_3},{C_4},...\;\) là \({a_1} = 4;{a_2} = \sqrt {10} ;{a_3} = \frac{5}{2};{a_4} = \frac{{5\sqrt {10} }}{8};...\)
Độ dài cạnh của hình vuông thứ n là: \({a_n} = \frac{{\sqrt {10} }}{4}{a_{n - 1}}\).
Vậy \(\frac{{{a_n}}}{{{a_{n - 1}}}} = \frac{{\sqrt {10} }}{4} = q\)
Vậy (an) là một cấp số nhân với số hạng đầu \({a_1} = 4\) và công bội \(q = \frac{{\sqrt {10} }}{4}\)
Cho một hình vuông có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để được một hình vuông, tiếp tục làm như thế đối với hình vuông mới (như hình vẽ bên).
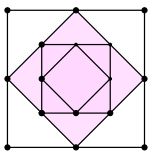
Tổng diện tích cách hình vuông liên tiếp đó là
A. 2
B. 3 2
C. 8
D. 4
Đáp án A
Theo giả thiết, diện tích hình vuông sau sẽ bằng 1 2 diện tích hình vuông trước.
Khi đó, tổng diện tích cần tính là tổng của cấp số nhân với u 1 = 1 , , với công bội q = 1 2 .
Vậy tổng S = u 1 1 − q n 1 − q = 1 1 − 2 − n 1 − 1 2
mà n → + ∞ ⇒ 2 − n → 0 suy ra S=2
Cho hình vuông có cạnh 4cm. Nối trung điểm của các cạnh ta được hình vuông thứ nhất . Nối trung điểm các cạnh ta được hình vuông thứ hai. Từ hình vuông thứ hai ta cũng làm như vậy để được hình vuông thứ ba... Cứ như thế để được hình vuông thứ 5 thì dừng lại. Tìm tổng diệntichs 5 hình vuông đó?
AI LƯỚT QUA ĐỂ LẠI CHO MK LỜI GIẢI NHA.CÁM ƠN NHÌU.
Số cây cam là:
120 : ( 2 + 3 ) x 2 = 48 (cây)
Số cây xoài là:
( 1 + 5 ) = 20 ( cây )
Số cây chanh là:
120 - ( 48 + 20 ) = 52 ( cây )
Đáp số : cam : 48 cây
xoài : 20 cây
chanh : 52 cây.
ai trên 10 điểm thì mình nha
Một hình vuông C 1 cạnh bằng a. Chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để được hình vuông C 2 (như hình vẽ bên). Tiếp tục như thế ta được dãy các hình vuông C 1 , C 2 , C 3 ,... Gọi Si là diện tích của các hình vuông C i (i=1,2,...). Tìm a biết S 1 + S 2 + . . . + S n + . . . = 96 .

A. 3.
B. 6.
C. 9.
D. 4.
cho một hình vuông abcd có diện tích là 64 cm2. Nối 4 trung điểm của các cạnh hình vuông ta được hình vuông thứ 1. nối 4 trung điểm của các cạnh hình vuông thứ 1 ta được hình vuông thứ 2. Tính diện tích hình vuông thứ 2
Nối trung điểm các cạnh hình vuông thì ta được hình vuông mới bằng nửa hình vuông ban đầu (xem hình vẽ)
(Các bạn có thể chứng minh bằng cách diện tích hình vuông trong bằng 4 tam giác cộng lại, bốn tam giác này lần lượt bằng bốn tam giác góc hình vuông to).
Cứ như vậy, ta tính được diện tích hình vuông cần tìm là: 64 : 2 : 2 = 16
cho hình vuông có cạnh 4 cm nối trung điểm của các cạnh ta được hình vuông thứ nhất nối trung điểm các cạnh của hình vuông thứ nhất ta được hình vuông thứ hai từ hình vuông thứ hai ta cũng làm như vậy để được hình vuông thứ ba cứ như thế để được hình vuông cứ như thể ta được hình vuông thứ năm thì dừng lại tìm tổng diện tích của 5 hình vuông đó
dien h hinh vuong lon gap 4 lan dien h hinh vuong thu nhat,dien h hinh vuong thu nhat gap 4 lan dien h hinh vuong thu 2 cu nhu the nen dien h hinh vuong thu 4 gap 4 lan dien h hinh vuong thu 5
tu do ta tinh duoc dien h hinh vuong thu nhat la 4
--------------------------------------------------------thu hai la 1
--------------------------------------------------------thu ba la 0,25
--------------------------------------------------------thu tu la 0,0625
--------------------------------------------------------thu nam la 0,015625
roi cong tat ca lai ta duoc 5,328125