Đáp án C

Áp dụng định lí pytago ta có:

a:

BC=35cm 

\(AH=\dfrac{AB\cdot AC}{BC}=16.8\left(cm\right)\)

b: \(AE=\dfrac{AH^2}{AC}=\dfrac{16.8^2}{28}=10.08\left(cm\right)\)

\(AD=\dfrac{AH^2}{AB}=\dfrac{16.8^2}{21}=13.44\left(cm\right)\)

Do đó: \(S_{AED}=\dfrac{AD\cdot AE}{2}=\dfrac{13.44\cdot10.08}{2}=67.7376\left(cm^2\right)\)

Ta có: ΔABC vuông tại A(gt)

nên \(\widehat{C}+\widehat{ABC}=90^0\)(hai góc nhọn phụ nhau)

hay \(\widehat{ABC}=50^0\)

\(\Leftrightarrow\widehat{ABD}=25^0\)

Xét ΔABD vuông tại A có 

\(AB=BD\cdot\cos\widehat{ABD}\)

\(\Leftrightarrow BD=\dfrac{21}{\cos25^0}\simeq23.2\left(cm\right)\)

a) Theo hệ thức liên hệ giữa đường cao và hình chiếu , ta có : AH2 = BH . CH

=> CH = AH2/BH = \(\dfrac{162}{25}=10,24\)

BC = BH + CH = 25 + 10,24 = 35,24

- Theo hệ thức liên hệ giữa cạnh góc vuông và hình chéo , ta có :

AB2 = BH.BC

=> AB\(\sqrt{\left(BH.BC\right)}\) 

= \(\sqrt{\left(25.35,24\right)}\)

= \(\sqrt{881=29,68}\)

AC2 = HC.BC

=> AC = \(\sqrt{\left(CH.BC\right)}\)

= \(\sqrt{\left(10,24.35,24\right)=}\sqrt{\left(360,9\right)=18,99}\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=21^2+28^2=1225\)

hay BC=35(cm)

Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất đường phân giác của tam giác)

hay \(\dfrac{BD}{21}=\dfrac{CD}{28}\)

mà BD+CD=BC(D nằm giữa B và C)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{BC}{49}=\dfrac{35}{49}=\dfrac{5}{7}\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{BD}{21}=\dfrac{5}{7}\\\dfrac{CD}{28}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=15\left(cm\right)\\CD=20\left(cm\right)\end{matrix}\right.\)

Vậy: BD=15cm; CD=20cm

Bài 3:

Ta có:

\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\)

\(\Rightarrow\widehat{P}=180^o-90^o-37^o=53^o\)  

Mà: \(sinN=\dfrac{MN}{NP}\)

\(\Rightarrow sin37^o=\dfrac{MN}{25}\)

\(\Rightarrow MN=25\cdot sin37^o\approx15\left(cm\right)\)

Áp dung định lý Py-ta-go ta có:

\(MP=\sqrt{NP^2-MN^2}=\sqrt{25^2-15^2}=20\left(cm\right)\)

3:

a: Xét ΔABC có AC^2=BA^2+BC^2

nên ΔBAC vuông tại B

b: Xét ΔBAC vuông tại B có

sin A=BC/AC=42/58=21/29

cos A=AB/AC=40/58=20/29

tan A=BC/BA=21/20

cot A=BA/BC=20/21

c: Xét ΔABC vuông tại B có BH là đường cao

nên BH*AC=BA*BC; BA^2=AH*AC; CB^2=CH*CA

=>BH*58=40*42=1680

=>BH=840/29(cm)

BA^2=AH*AC

=>AH=BA^2/AC=40^2/58=800/29cm

CB^2=CH*CA

=>CH=CB^2/CA=42^2/58=882/29(cm)

ΔBHA vuông tại H có HE là đường cao

nênBE*BA=BH^2

=>BE*40=(840/29)^2

=>BE=17640/841(cm)

ΔBHC vuông tại H có HF là đường cao

nênBF*BC=BH^2

=>BF*42=(840/29)^2

=>BF=16800/841(cm)

Xét tứ giác BEHF có

góc BEH=góc BFH=góc EBF=90 độ

=>BEHF là hình chữ nhật

=>góc BFE=góc BHE(=1/2*sđ cung BE)

=>góc BFE=góc BAC

Xét ΔBFE và ΔBAC có

góc BFE=góc BAC

góc FBE chung

Do đó: ΔBFE đồng dạng với ΔBAC
=>S BFE/S BAC=(BF/BA)^2=(16800/441:40)^2=(420/841)^2

=>S AECF=S ABC*(1-(420/841)^2)

=>\(S_{AECF}=\dfrac{1}{2}\cdot40\cdot42\cdot\left[1-\left(\dfrac{420}{841}\right)^2\right]\simeq630,5\left(cm^2\right)\)

Đã đăng lên cộng đồng thì phải nhờ đến tất cả chứ bạn, nếu nhờ riêng ai đó thì mời ib?

Đăng như vậy có ngày không ai giúp bạn đâu.

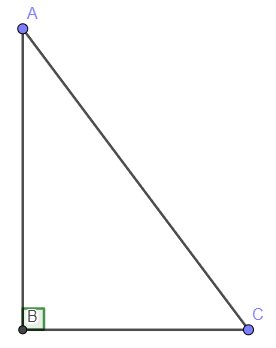
a, \(sin\left(A\right)=\dfrac{BC}{AC}\Leftrightarrow sin\left(40^o\right)=\dfrac{BC}{8}\Leftrightarrow BC\approx5,14\left(cm\right)\)
\(cos\left(A\right)=\dfrac{AB}{AC}\Leftrightarrow cos\left(40^o\right)=\dfrac{AB}{8}\Leftrightarrow AB\approx6,12\left(cm\right)\)
b,
\(cotg\left(C\right)=\dfrac{BC}{AB}\Leftrightarrow\dfrac{1}{\sqrt{3}}=\dfrac{BC}{5}\Leftrightarrow BC=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)