Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC. Tính A H → . C A →
A. 3 a 2 4
B. - 3 a 2 4
C. 3 a 2 2
D. - 3 a 2 2
Những câu hỏi liên quan
Cho tam giác ABC cân tại A, đường cao AH (H thuộc BC )a, tam giác ABH bằng tam giác ACH. B, lấy K là trung điểm của AC gọi g là giao điểm của AH và BK điểm g có cách đều ba cạnh của tam giác ABC không? vì sao? c, AC = 2 cm tính AH=? (Hãy nêu giả thiết và kết luận và vẽ hình)
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: G ko cách đều ba cạnh của ΔABC vì G ko phải là tâm đường tròn nội tiếp tam giác
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng cách từ điểm D đến đường thẳng BC là a . Gọi H là trung điểm BC, I là trung điểm AH. Tính khoảng cách giữa AD và BC.
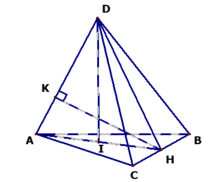
Tính khoảng cách giữa AD và BC.
● Trong ΔADH vẽ đường cao HK tức là HK ⊥ AD (1)
- Mặt khác BC ⊥ (ADH) nên BC ⊥ HK (2)
- Từ (1) và (2) ta suy ra d(AD, BC) = HK.
● Xét ΔDIA vuông tại I ta có:
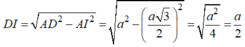
● Xét ΔDAH ta có:
Đúng 0
Bình luận (0)
Cho tam giác ABC đều cạnh a ; H là trung điểm của BC. Tính
C
A
→
−
H
C
→
.
A.
C
A
→
−
H
C...
Đọc tiếp
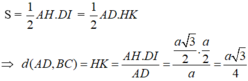
Cho tam giác ABC đều cạnh a ; H là trung điểm của BC. Tính C A → − H C → .
A. C A → − H C → = a 2 .
B. C A → − H C → = 3 a 2 .
C. C A → − H C → = 2 3 a 3 .
D. C A → − H C → = a 7 2 .
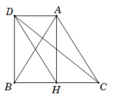
Gọi D là điểm thỏa mãn tứ giác ACHD là hình bình hành
⇒ A H B D là hình chữ nhật.
C A → − H C → = C A → + C H → = C D → = C D .
C D = B D 2 + B C 2 = A H 2 + B C 2 = 3 a 2 4 + a 2 = a 7 2 .
Đáp án D
Đúng 0
Bình luận (0)
Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính
C
A
→
-
H
C
→
A. B. C. D.
Đọc tiếp
Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính C A → - H C →
A. 
B. 
C. 
D. 
Cho tam giác ABC đều cạnh a; H là trung điểm của BC. Tính
C
A
→
−
H
C
→
.
A.
C
A
→
−
H...
Đọc tiếp
Cho tam giác ABC đều cạnh a; H là trung điểm của BC. Tính C A → − H C → .
A. C A → − H C → = a 2 .
B. C A → − H C → = 3 a 2 .
C. C A → − H C → = 2 3 a 3 .
D. C A → − H C → = a 7 2 .
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a Hình chiếu vuông góc của S lên (ABC )trùng với trung điểm H của cạnh BC biết tam giác SBC là tam giác đều tính số đo của góc giữa SA và (ABC)
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều SBC cạnh a)
\(AH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều ABC cạnh a)
\(tan\widehat{SAH}=\dfrac{SH}{AH}=1\Rightarrow\widehat{SAH}=45^0\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC) A. 300 B. 450 C. 600 D. 900
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)
A. 300
B. 450
C. 600
D. 900
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên
(
A
B
C
)
trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và
(
A
B
C
)
.
A.
30
0
B.
45
0
C.
60
0
D. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên ( A B C ) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và ( A B C ) .
A. 30 0
B. 45 0
C. 60 0
D. 90 0
Đáp án B
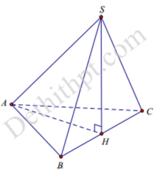
Vì hai tam giác ABC và SBC đều và có chung cạnh BC nên bằng nhau ⇒ A H = S H .
Mà Δ H S A vuông tại H nên vuông cân
⇒ S A H ^ = 45 °
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
A. 30 °
B. 75 °
C. 60 °
D. 45 °
