Tổng 3 góc của tam giác

Những câu hỏi liên quan
cho tam giác ABC vuông tại A kẻ BD là phân giác của góc B kẻ DH vuông góc với BC tại H biết tổng 3 góc trong tam giác BDH=180 độ biết góc ABC=60 độ góc ACB=30 độ và tổng 3 góc trong tam giác HDC=180 độ.Tính góc BDC
Số đo 3 góc của một tam giác tỉ lệ với 15; 6; 9. Tính số đo mỗi góc của tam giác biết tổng số đo 3 góc trong một tam giác bằng 180 độ.
gọi số đo 3 góc là a,b,c(a,b,c>0)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{15}=\dfrac{b}{6}=\dfrac{c}{9}=\dfrac{a+b+c}{15+6+9}=\dfrac{180^o}{30}=6^o\)
\(\dfrac{a}{15}=6^o\Rightarrow a=90^o\\ \dfrac{b}{6}=6^o\Rightarrow b=36^o\\ \dfrac{c}{9}=6^o\Rightarrow c=54^o\)
Đúng 1
Bình luận (2)
Gọi 3 góc của tam giác là a,b,c(độ;a>b>c>0)
Áp dụng tc dtsbn:
\(\dfrac{a}{15}=\dfrac{b}{9}=\dfrac{c}{6}=\dfrac{a+b+c}{15+6+9}=\dfrac{180}{30}=6\\ \Leftrightarrow\left\{{}\begin{matrix}a=90\\b=54\\c=36\end{matrix}\right.\)
Vậy ...
Đúng 0
Bình luận (2)
Gọi số đo từng góc của tam giác là: x,y,z(bạn đặt đk nhé)
ta có: \(\dfrac{x+y+z}{15+6+9}=\dfrac{180}{30}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=6.15=90\\y=6.6=36\\z=6.9=54\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tam giác ABC có số đo 3 góc A, B , C tỉ lệ với 3; 5 ;7. Tính số đo các góc của tam giác ABC (biết rằng tổng số đo 3 góc trong một tam giác bằng 180o)
Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
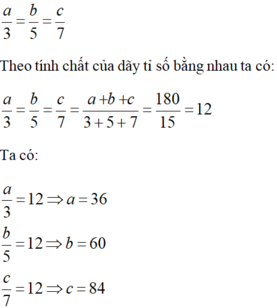
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o
Đúng 0
Bình luận (0)
a nhắc lại định lý tổng 3 góc trong một tam giác
b vẽ tứ giác ABCD tùy ý dựa vào định lí về tổng 3 góc của 1 tam giác hãy tính tổng
cho tam giác ABC tại mỗi đingr vẻ một góc ngoài của tam giác tính tổng số đo 3 góc ngoài
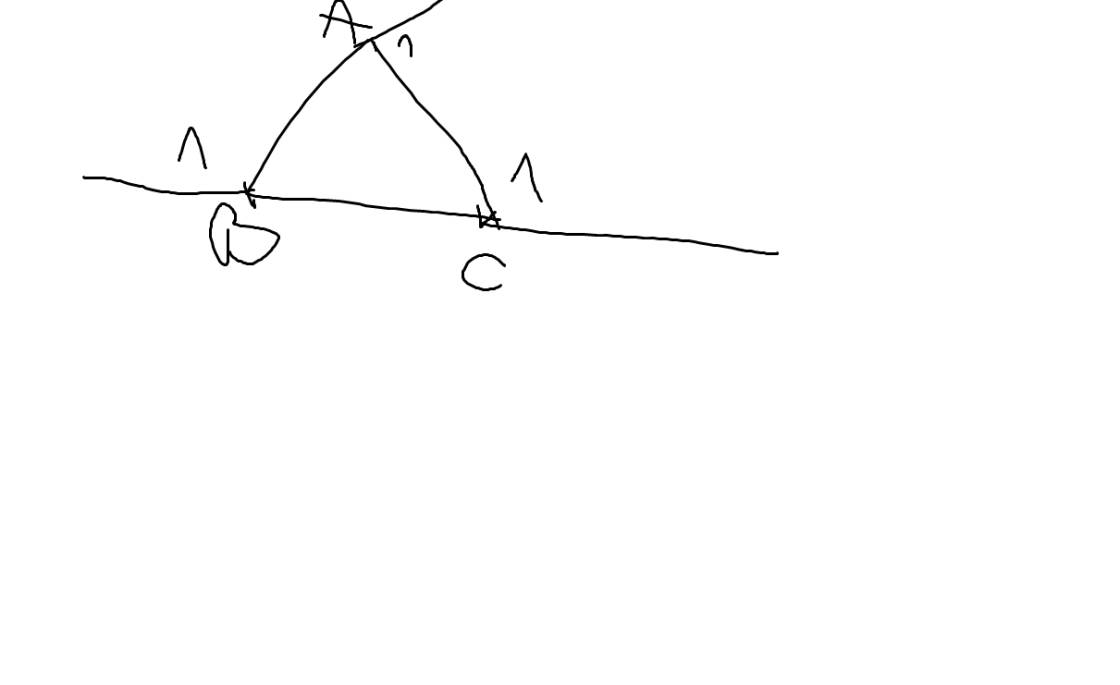
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)
Đúng 1
Bình luận (0)
1) Tính tổng các góc ngoài của ngũ giác ABCDE?
2)tính tổng các góc ngoài của tam giác ABC
3)nhận xét về toongrcacs góc ngoài của đa giác
Tìm các góc của 1 tam giác biết rằng các góc của nó tỉ lệ với 1, 2, 3. (Tổng các góc trong tam giác bằng 180 độ)
Gọi ba góc của tam giác là a,b,c
Theo bài ra,ta có :
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\) và a + b + c = 180
Theo dãy tỉ số bằng nhau,ta có :
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}=\frac{180}{6}=30\)
=> a = 1.30 = 30o
b = 2.30 = 60o
c = 3.30 = 90o
Chúc bạn học tốt
Đúng 0
Bình luận (0)
Gọi 3 góc của tam giác là A ; B ; C
=> \(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}\) ; A + B + C = 180 độ
áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{A+B+C}{1+2+3}=\frac{180}{6}=30\)
\(\Rightarrow A=30\cdot1=30\)
\(\Rightarrow B=30\cdot2=60\)
\(\Rightarrow C=30\cdot3=90\)
Vậy ...
Đúng 0
Bình luận (0)
Goi so do 3 goc lan luot la a,b,c
Co a/1 = b/2 = c/3 = a+b+c/1+2+3 = 1800 / 6 = 300
a = 300 . 1= 300
b = 300 . 2 = 600
c = 300 . 3 = 900
KL : ...
Đúng 0
Bình luận (0)
1.Khẳng định nào sau đây không đúng:
A. Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó
B. Trong tam giác cân hai góc ở đáy bằng nhau
C. Tam giác có hai góc bằng nhau là tam giác đều
2.Tam giác nào là tam giác vuông với số đo 3 cạnh như sau:
A. 13m; 14m; 15m B. 11m; 12m; 10m
C. 12m; 9m; 15m D. 8m; 8m; 10m
D. Trong tam giác đều mỗi góc bằng 60 độ
1.Khẳng định nào sau đây không đúng:
A. Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó
B. Trong tam giác cân hai góc ở đáy bằng nhau
C. Tam giác có hai góc bằng nhau là tam giác đều
2.Tam giác nào là tam giác vuông với số đo 3 cạnh như sau:
A. 13m; 14m; 15m B. 11m; 12m; 10m
C. 12m; 9m; 15m D. 8m; 8m; 10m
D. Trong tam giác đều mỗi góc bằng 60 độ
Đúng 2
Bình luận (0)























